✔ ▶ Examen de 3 ESO (Global 1º Ev 20/21) 📑 🚩

A continuación te resuelvo el examen global de la primera evaluación de 3ESO del curso 2020-2021

Ejercicio 1

Vas a comprar aceite de oliva y te encuentras una oferta de \texttt{2×1: lleva dos unidades y paga sólo la primera}. En el mismo estante te encuentras otra oferta que dice \texttt{Lleva tres y te hacemos un 70\% en la tercera unidad}. ¿cuál de las ofertas es con la que más ahorras?

En este ejercicio te plantean un problema que te puede ocurrir en el día a día: comparar dos ofertas a ver cuál te interesa más. Si quieres leer la entrada sobre los porcentajes, puedes hacerlo aquí.

Vamos con el ejercicio:

Hay varias formas de acercarse a este ejercicio. Te lo haré de dos maneras diferentes:

Primera forma.

Supongamos que lo que la botella de aceite de oliva cuesta 1€ (cuesta más, pero lo importante es tener una cantidad con la que trabajar).

1º Oferta: 2×1. Te llevas dos botellas y pagas 1€. Cada botella «cuesta» 0.5€.
2º Oferta: Lleva 2 y en la tercera tienes un 70%. Te llevas 3 botellas y pagas 1+1+0.3=2.3€. Cada botella «cuesta» 0.77€

Por tanto la oferta con la que más ahorras es la primera. Ahorras un 50%.

Segunda forma

Básicamente es lo mismo que acabamos de hacer, pero con un lenguaje más técnico.

Supongamos ahora que el precio de la botella es $P$ .

1º Oferta: compras dos botellas y pagas $P$ , es decir que cada botella «cuesta» $\displaystyle \frac{P}{2}$
2º Oferta: compras tres botellas y pagas $P+P+0.3P=2.3P$ . Así cada botella «cuesta» $\displaystyle \frac{2.3\cdot P}{3}$

¿Qué oferta es mejor? Vamos a dividir ambos precios y ver si nos da un resultado mayor o menor que uno.

$\frac{Oferta\ 1}{Oferta \ 2}=\frac{\frac{P}{2}}{\frac{2.3\cdot P}{3}}=\frac{15}{23}<1$

Como el resultado que obtenemos es menor que uno, esto significa que el numerador es menor que el denominador. O lo que es lo mismo, con la oferta 1 pagas menos.

Como ves llegamos al mismo resultado.

Ejercicio 2

Una planta perenne genera 5 semillas y al año siguiente cada una de las plantas hijas, genera otras cinco semillas y así sucesivamente. ¿Cuántas plantas hay al cabo de 10 años? (NOTA: no calcules las potencias. Déjalo indicado. Si quieres calcularlo necesitas saber que $5^9=1953125$ )

Se trata de calcular el término número 10 de una progresión geométrica.

Simplemente hay que aplicar la fórmula y ya está. Además no te pido que lo calcules, sólo déjalo indicado (no obstante ya sé que alguien va a querer calcularlo, y como no dejo calculadora en los exámenes, por eso te digo cuánto es $5^9$ . Por cierto es una pistaza )

$g_n=g_1\cdot r^{n-1}$

Como nos piden el año 10, tenemos que $n=10$ . Además, como cada planta genera 5 semillas, tenemos que $r=5$ . Por otro lado, como empezamos con una planta: $g_1=1$

$g_{10}=1\cdot 5^{10-1}=5^9=<strong>1953125</strong>$

Ejercicio 3

Simplifica: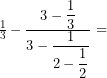
$\frac{1}{3}-\frac{\displaystyle3-\frac{1}{3} }{\displaystyle3-\frac{1}{\displaystyle 2-\frac{1}{2}}}=$
$\sqrt[3]{16\cdot 12\cdot 36\cdot 343}=$

Se trata de un ejercicio de aritmética sencillo para 3ESO.

Apartado A: $\displaystyle \frac{1}{3}-\frac{\displaystyle3-\frac{1}{3} }{\displaystyle3-\frac{1}{\displaystyle 2-\frac{1}{2} } }=$

$\displaystyle\frac{1}{3}- \frac{ \displaystyle 3-\frac{1}{3} }{ \displaystyle 3- \frac{ 1 }{ \displaystyle 2-\frac{1}{2} } } = \frac{1}{3}- \frac{ \displaystyle \frac{9-1}{3} }{ 3-\displaystyle \frac{ 1 }{ \displaystyle \frac{4-1}{2} } } =\frac{1}{3}-\frac{ \displaystyle \frac{8}{3} }{ \displaystyle 3-\frac{2}{3} }=$

Seguimos operando:

$\displaystyle \frac{1}{3}-\frac{\displaystyle\frac{8}{3}}{3-\frac{2}{3}}=\frac{1}{3}-\frac{\displaystyle\frac{8}{3}}{\displaystyle\frac{9-2}{3}}=\frac{1}{3}-\frac{8}{7}=$

Y de aquí obtenemos que:

$\frac{7-24}{21}=-\frac{17}{21}$

Apartado B: $\sqrt[3]{16\cdot 12\cdot 36\cdot 343}=$

La única dificultad aquí estriba en factorizar $343=7^3$ porque la factorización de los demás números debe ser trivial en 3ESO.

$\sqrt[3]{16\cdot 12\cdot 36\cdot 343}=\sqrt[3]{2^4\cdot 2^2\cdot 3\cdot 2^2\cdot 3^2\cdot 7^3}=\sqrt[3]{2^8\cdot 3^3\cdot 7^3}=2^2\cdot 3\cdto 7\sqrt[3]{2^2}$

Este ejercicio, puesto que se trata de saber si sabes operar, para mi ya está completamente hecho. Sin embargo, debido a que los números son muy manejables, no estaría de más que escribieses que tu solución es:

$84\sqrt[3]{4}$

Ejercicio 4

Alicia estaba conversando con el Gato de Cheshire, cuando vio pasar a su lado la Liebre de Marzo a una velocidad de $10\ km/h$ . Como tenía que contarle una historia, apenas $10\ s$ después Alicia salió corriendo detrás de la liebre a $15\ km/h$ . La madriguera de la liebre está situada a $100\ m$ de donde está Alicia, ¿podrá alcanzar a la liebre antes de que entre en la madriguera?

Este ejercicio lo puedes ver resuelto aquí. Así que no te lo voy a volver a resolver

Ejercicio 5

20 obreros trabajando 7 horas al día tardan 8 días en construir una caseta. Si sólo disponemos de 14 obreros y 10 días, cuántas horas necesitarían trabajar al día para realizar la misma obra?

Se trata de un problema de proporcionalidad compuesta, así que lo primero que debes hacer es elaborar tu tabla:

Situación	Obreros	Días	Horas
Enunciado	20	8	7
Problema	14	10	x

Tabla resumen del problema.

Lo siguiente que debes ver es cómo se relacionan las variables de las que tienes información, con la variable hora:

Obreros-Horas: INVERSA. Porque cuantos más obreros haya, menos horas se va a tardar.
Dias-Horas: INVERSA. Porque cuantos más días tengas, menos horas debes trabajar para acabar a tiempo.

Así que ahora planteamos nuestro problema:

$\frac{20}{14}\cdot\frac{8}{10}=\frac{x}{7}$

Sólo hay que operar y tenemos:

$x=\displaystyle \frac{20}{14}\cdot\frac{8}{10}}\cdot 7=8$

Así pues, habría que trabajar 8 horas al día.

Y con esto se acabó la entrada de hoy, pero antes de despedirme, déjame que me eche unas flores y te diga que el examen está puesto para que apruebe hasta el que no quiere…

Y ahora sí, hasta aquí la entrada de hoy, si quieres estar al loro de lo que ocurre en el blog, suscríbete al boletín

Si quieres contactar conmigo puedes hacerlo aquí

Si te gusta lo que hago y quieres invitarme a un café ¡¡te doy las gracias por adelantado!!

Gracias por leerme