Examen 3ESO (2Ev 1Ex 2020-21)

En la entrada de hoy te voy a resolver un examen de 3ESO de la segunda evaluación

Pregunta 1

Resuelve los siguientes productos notables (pregunta de todo o nada)

$\displaystyle (x-2)^2$
$\displaystyle 5-x^2$
$\displaystyle x^2-3x+\frac{9}{4}$

$\displaystyle (2+x)(2-x)$
$\displaystyle x^2+2x+1$
$\displaystyle (3x+2)^2$

Esta pregunta es muy sencilla de responder pues se trata simplemente de saber si conoces los productos notables que como ya te he dicho otras veces SON IMPRESCINDIBLES para aprobar la asignatura (tanto en 3ESO, como en 4ESO).

La resolución se basa en las siguientes fórmulas que puedes leer de izquierda a derecha y de derecha a izquierda:

$(a\pm b)^2 = a^2 \pm 2ab + b^2$
$(a+b)(a-b)=a^2-b^2$

Así que las soluciones son:

$\displaystyle (x-2)^2= \color {blue} x^2-4x+4$
$\displaystyle 5-x^2= \color {blue} (\sqrt{5}-x)(\sqrt{5}+x)$
$\displaystyle x^2-3x+\frac{9}{4}= \color {blue}\left(x-\frac{3}{2}\right)$
$\displaystyle (2+x)(2-x)= \color {blue} 4-x^2$
$\displaystyle x^2+2x+1= \color {blue} (x+1)^2$
$\displaystyle (3x+2)^2= \color {blue} (3x+2)^2$

Pregunta 2

Sean los polinomios $A(x)$ , $B(x)$ y $C(x)$ . Calcula $-2xA(x)+B(x)C(x)$

$A(x)=-x^5+x^4-2x^3+3x^2-5x+1$
$B(x)=-x^4+2x-3$
$C(x)=-x^2-2$

La aritmética de los polinomios ya te la he explicado en esta entrada, así que te remito a ella para la parte teórica. Ahora solo te voy a poner los resultados finales:

$\begin{aligned} -2xA(x) &= 2x^6-2x^5+4x^4-6x^3+10x^2-2x\\ B(x)\cdot C(x) &= x^6+2x^4-2x^3-4x+6\\\hline -2xA(x)+B(x)\cdot C(x)&= 3x^6-2x^5+6x^4-8x^3+10x^2-6x +6 \end{aligned}$

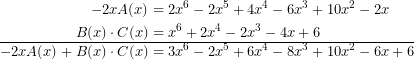
Y ese es el resultado.

Pregunta 3

Dado el polinomio $P(x)=9x^4-9x^3-ax^2+2x+12$ calcula el valor de $a$ para que $x=3$ sea una raíz del polinomio.

En este caso puedes plantear el sistema de dos formas diferentes (aunque en el fondo son la misma):

Primera forma: Usando el teorema del resto

Como ya te expliqué en esta entrada, podemos usar el teorema del resto para factorizar este polinomio de la siguiente manera:

Debido a que $x=3$ tiene que ser raíz del polinomio, eso significa que $(x-3)$ es un factor del mismo, o lo que es lo mismo que $P(3)=0$ . Así pues, no tenemos más que sustituir la $x$ por un $3$ y luego igualar a $0$ (recuerda que nuestra incógnita es $a$ ).

$P(3)=9\cdot 3^4-9\cdot 3^3-a\cdot 3^2+2\cdot 3+12=504+9a====0$

Y de aquí se deduce que $\displaystyle a=\frac{504}{9}=56$

Segunda forma: Usando la regla de Ruffini

En esta entrada te expliqué qué es la regla de Ruffini, por qué funciona y cómo se usa. Así que vamos a pasar a aplicarla directamente:

$\text{\begin{tabular}{c|ccccc}\color{red}$ $&\color{red}$9 $&\color{red}$ -9$&\color{red}$-a $&\color{red}$2 $&\color{red}$12 $\\\\\color{blue}$3 $&$ $&$27 $&$54 $&$162-3a $&$492-9a $\\\hline \\$ $& \color{orange}$9 $&\color{orange}$18 $&\color{orange}$ 54-a$&$\color{orange}164-3a $ &${\hspace*{-11pt}}\vline \hspace*{7pt}\color{green!60!black} 504-9a$\\\cline{6-6}\end{tabular}}$

Y como ves, llegamos a la misma pregunta y es ¿cuánto vale $a$ para que $504-9a=0$ ?

Y, lógicamente la respuesta es la misma:

$a=56$

Pregunta 4

Supón que en el ejercicio anterior has obtenido $P(x)=9x^4-9x^3-56x^2+2x+12$ . Factorízalo hallando todas sus raíces y factores. Expresa el polinomio correctamente factorizado.

En este ejercicio te daba una pista maravillosa, te estaba diciendo que en el polinomio anterior $a=56$ , así que podías saber antes de entregar el examen si lo tenías bien o lo tenías mal.

Pero en fin, en esta pregunta te pedían factorizar el polinomio, del que ya sabes una respuesta $x=3$ es un factor, así que lo primero que vamos a hacer es utilizar Ruffini, para dividir $P(x): (x-3)$

$\text{\begin{tabular}{c|ccccc}\color{red}$ $&\color{red}$9 $&\color{red}$ -9$&\color{red}$-56 $&\color{red}$2 $&\color{red}$12 $\\\\\color{blue}$3 $&$ $&$27 $&$54 $&$-6 $&$-12 $\\\hline \\$ $& \color{orange}$9 $&\color{orange}$18 $&\color{orange}$ -2$&$\color{orange}-4 $ &${\hspace*{-11pt}}\vline \hspace*{7pt}\color{green!60!black} 0$\\\cline{6-6}\end{tabular}}$

Por lo que ya tenemos localizada nuestra primera solución $x_1=3$ (que ya conocíamos).

Y ahora ya sabemos que $P(x)=(9x^3+18x^2-2x-4)\cdot (x-3)$ Y ahora sí, nos peleamos con el polinomio $Q(x)=9x^3+18x^2-2x-4$

Los divisores del término independiente son $D(-4)=\{\pm 1, \pm 2, \pm 4\}$
Si probamos con Ruffini vemos que el único que «nos sirve» es $x=-2$

$\text{\begin{tabular}{c|cccc}\color{red}$ $&\color{red}$9 $&\color{red}$ 18$&\color{red}$-2 $&\color{red}$2 $\\\\\color{blue}$-2 $&$ $&$-18 $&$0 $&$4 $\\\hline \\$ $& \color{orange}$9 $&\color{orange}$0 $&\color{orange}$ -2$&${\hspace*{-11pt}}\vline \hspace*{7pt}\color{green!60!black} 0$\\\cline{5-5}\end{tabular}}$

Bien, nuestra segunda solución es $x_2=-2$ , vamos a ver si podemos conseguir las otras soluciones.

Con lo que ahora nos queda ver qué hacemos con el polinomio $R(x)= 9x^2-2$ Pero resulta que si lo igualamos a cero obtenemos una ecuación de segundo grado, así que vamos a resolverla:

$9x^2-2=0\Longrightarrow x=\sqrt{\frac{2}{9}}$

Por lo que las soluciones son:

$x_3=\frac{\sqrt{2}}{3}\qquad x_4=-\frac{\sqrt{2}}{3}$

Así que ahora que conocemos todas las raíces del polinomio, nos queda expresar $P(x)$ de forma factorizada:

$P(x)= 9(x-3)(x+2)\left(x-\frac{\sqrt{2}}{3}\right)\left(x+\frac{\sqrt{2}}{3}\right)$

Pregunta 5

Opera las siguientes fracción algebraica dejando el resultado tan simplificado como sea posible.

$\frac{x^2-2}{x^3-3x^2+3x-1}\cdot \frac{x^2-2x+1}{x^2-2\sqrt{2}x+2}+\frac{x^2-2x+3}{x^2-x-2}$

Esta pregunta es fácil y difícil a la vez: es fácil porque no se puede simplificar mucho la expresión que te doy; y es difícil porque la mayoría de los alumnos se empeñan en que aparezca algo así como $\displaystyle \frac{x-3}{2x^2-1}$ lo cual no va a ocurrir, y eso hace que la gente empiece a dar vueltas y más vueltas al ejercicio sin llegar a ningún sitio.

Debo reconocer que este no era el ejercicio que programé en un primer momento si no que me bailaron algunos coeficientes y por ello no se podía simplificar tanto como yo hubiese deseado.

Pero esto no significa que no podamos operar. Lo primero es factorizar todos los polinomios que aparecen en esta expresión para así poder simplificar lo que se pueda.

$\frac{\left(x+\sqrt{2}\right)\color{blue}\left(x-\sqrt{2}\right)}{\left(x-1\right)^{\color{red}3}}\cdot\frac{\color{red}\left(x-1\right)^2}{\left(x-\sqrt{2}\right)^{\color{blue}2}}+\frac{x^2-2x+3}{(x+1)(x-2)}$

Te he coloreado lo que se va a simplificar. Y así te queda:

$\frac{x+\sqrt{2}}{x-1}\cdot\frac{1}{x-\sqrt{2}}+\frac{x^2-2x+3}{(x+1)(x-2)}$

Con llegar hasta aquí (1 paso) para mí era suficiente, pues demostrabas que sabías qué había que hacer frente a una fracción algebraica. Unirlo todo en una única fracción suponía hacer una serie de operaciones que solo nos iban a llevar a un churrofórmula al que no era necesario enfrentarse.

Y hasta aquí la entrada de hoy. Espero que te haya servido y ya sabes que si quieres mantenerte informado de más cuestiones puedes suscribirte al boletín

Si quieres contactar conmigo puedes hacerlo aquí

Si te gusta lo que hago y quieres invitarme a un café ¡¡te doy las gracias por adelantado!!

Gracias por leerme

Vida de la entrada:

– 2021-04-12: Publicación.
–