▶🎖 Factorización de polinomios 📚
¡¡Factorización de polinomios!! 😨 ¡¿En serio te han mandado factorizar polinomios!? ¿¡Y no se puede hacer con calculadora?! Lamento decirte que ambas respuestas son afirmativas. Te va a tocar factorizar polinomios, y además, no vas a poder usar calculadora, porque para esto no sirve. Hay muchas cosas más para las que la calculadora no sirve, por ejemplo, decir cuántas cifras tiene ![]() o bien qué número es mayor el anterior o
o bien qué número es mayor el anterior o ![]() ¡¡Bienvenido a las matemáticas 🎉, donde lo importante es pensar 🤔 y no calcular 🧮!!
¡¡Bienvenido a las matemáticas 🎉, donde lo importante es pensar 🤔 y no calcular 🧮!!
Esta entrada es continuación de otra de introducción a los polinomios y puedes seguir leyendo la dedicada a la regla de Ruffini en donde te explico exactamente cómo factorizar un polinomio.
El objetivo de esta entrada no es tanto llegar a la factorización de un polinomio en sí, ya que eso (el cómo se factoriza de forma práctica) te lo explico con la regla de Ruffini; sino contarte qué requisitos deben cumplir las raíces de un polinomio, la diferencia y relación entre raíz y factor de un polinomio. Es decir, en esta entrada te hablaré de qué debes saber antes de ponerte a factorizar un polinomio.
Por lo tanto, en esta entrada verás las siguientes cuestiones:
- Qué es una raíz de un polinomio
- Qué es un factor de un polinomio
- La relación existe entre una raíz y un factor de un polinomio
- Cuántas raíces puedes encontrar como máximo en un polinomio.
- Cómo se relacionan las raíces de un polinomio y el término independiente y el coeficiente director.
Qué debes saber en la ESO y bachillerato
La factorización de polinomios se empieza a ver en 3ESO. Si bien en 2ESO ya se ha introducido la multiplicación y la división; lo cierto es que es en 3ESO cuando se ve la división de polinomios en toda su extensión (se dividen polinomios entre polinomios) y se empieza a ver la factorización. Es en 4ESO cuando llueve sobre mojado y se fijan todos los conceptos vistos en cursos anteriores.
¿Qué es factorizar un polinomio?
Factorizar un polinomio es calcular sus factores primos. ¡Hala! ya está.
Pero esta frase, por sí misma no dice gran cosa. Voy a empezar igual que hago en clase, mostrándote qué es factorizar un número. Tengo varias entradas sobre números primos que son esta, esta y esta. Al final lo importante es que sepas que un número se puede descomponer de manera única en producto de otros varios números que son primos.
Por ejemplo, ![]() o bien
o bien ![]() y también
y también ![]() . Sin embargo tenemos números primos que no se pueden descomponer en producto de otros dos como son
. Sin embargo tenemos números primos que no se pueden descomponer en producto de otros dos como son ![]() o bien
o bien ![]() o también
o también ![]() .
.
Con los polinomios y su factorización va a ocurrir lo mismo. Habrá algunos polinomios que los podamos descomponer en en producto de otros que denominaremos factores; mientras que otros polinomios serán factores primos.
En la ESO y bachillerato se aborda este tema trabajando con números reales, por lo que algunos polinomios primos tendrán grado 2. Sin embargo si trabajamos en el cuerpo de los complejos, todos los polinomios se podrán descomponer en factores primos de grado uno, como te comento más adelante.
Por ejemplo,
- el polinomio
 lo podrás factorizar como
lo podrás factorizar como  ;
; - o bien el polinomio
 lo vamos a factorizar como
lo vamos a factorizar como  ;
; - sin embargo, el polinomio
 lo acabarás factorizando como
lo acabarás factorizando como  . En este caso aparece un polinomio de grado 2
. En este caso aparece un polinomio de grado 2 ![Rendered by QuickLaTeX.com \left[x^2+x+4\right]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI3NCIgaGVpZ2h0PSIxOCIgdmlld0JveD0iMCAwIDc0IDE4Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBmaWxsPSIjY2ZkNGRiIi8+PC9zdmc+) que actúa como un factor primo, ya que es irreducible en el cuerpo de los números reales. La factorización, en números complejos, de este último polinomio es la siguiente:
que actúa como un factor primo, ya que es irreducible en el cuerpo de los números reales. La factorización, en números complejos, de este último polinomio es la siguiente:  . Si aún no has estudiado los números complejos y no entiendes muy bien esta última parte del párrafo, lo importante es que te quedes con que si trabajas con números reales, algunos factores primos de polinomios pueden tener grado dos.
. Si aún no has estudiado los números complejos y no entiendes muy bien esta última parte del párrafo, lo importante es que te quedes con que si trabajas con números reales, algunos factores primos de polinomios pueden tener grado dos.
Con esto lo que quiero mostrarte es que, al igual que para números, los polinomios pueden tener varios factores primos y algunos de ellos pueden estar repetidos.
El número de veces que aparece un mismo factor primo se va a llamar multiplicidad. Así, en el caso del polinomio ![]() anterior, la multiplicidad del factor
anterior, la multiplicidad del factor ![]() es tres, por esa razón está elevado al cubo; sin embargo en el polinomio
es tres, por esa razón está elevado al cubo; sin embargo en el polinomio ![]() , la multiplicidad del factor
, la multiplicidad del factor ![]() es tan solo de
es tan solo de ![]() y por eso está elevado al cuadrado. Por último en el polinomio
y por eso está elevado al cuadrado. Por último en el polinomio ![]() ese factor
ese factor ![]() no aparece, así que la multiplicidad es 0.
no aparece, así que la multiplicidad es 0.
¿Qué son las raíces de un polinomio?
Valor númérico de un polinomio
El valor numérico de un polinomio es aquel que se obtiene de sustituir la incógnita por el número en cuestión. Es decir, para el polinomio
![]()
![]()
Fíjate que ya no hemos puesto ![]() si no
si no ![]() , y al final todo se reduce en hacer unas pocas cuentas.
, y al final todo se reduce en hacer unas pocas cuentas.
Hay algunos valores numéricos que son muy fáciles de calcular:
- Si estás calculando el valor numérico de un polinomio
 para
para  , entonces
, entonces  (puedes pensar por qué
(puedes pensar por qué )
- Si quieres saber el valor numérico de un polinomio para
 , entonces
, entonces  (piensa también por qué
(piensa también por qué )
Te pongo una tabla con unos cuantos polinomios y el valor numérico para algunos números:
| Polinomio | |||||
| 0 | -2 | +2 | 0 | -4 | |
| 1 | 0 | 16 | 256 | 1 | |
| 0 | 0 | 0 | 0 | 0 | |
Como puedes comprobar en la tabla anterior, nada hay que te permita, a priori, saber si el valor numérico de un polinomio va a ser un número u otro. En concreto, en la tabla anterior he querido que siempre hubiese algún momento que el valor numérico fuese 0. Si eso ocurre, decimos que hemos encontrado una raíz.

![]() un polinomio y sea
un polinomio y sea ![]() el valor numérico del polinomio para
el valor numérico del polinomio para ![]() . Si
. Si ![]() decimos que
decimos que ![]() es raíz del polinomio
es raíz del polinomio
Es decir, que para buscar raíces de un polinomio tenemos que encontrar números que anulen su valor numérico.
Sin entrar en cuestiones de análisis matemático, te diré lo siguiente: Un polinomio lo puedes ver como una función continua (de hecho se denomina función polinómica) y así, encontrar una raíz de un polinomio equivale a encontrar los puntos de corte de esa función con el eje ![]() . Por ejemplo, puedes ver el siguiente gráfico, donde te he marcado el eje de abscisas y el de ordenadas.
. Por ejemplo, puedes ver el siguiente gráfico, donde te he marcado el eje de abscisas y el de ordenadas.

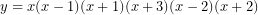 . Las raíces de esta función están marcadas con triangulitos azules sobre el eje de abscisas. Analizar las raíces de esta función es analizar las raíces del polinomio
. Las raíces de esta función están marcadas con triangulitos azules sobre el eje de abscisas. Analizar las raíces de esta función es analizar las raíces del polinomio ![Rendered by QuickLaTeX.com \[P(x)=x(x-1)(x+1)(x+3)(x-2)(x+2)=x^6+ 3x^5-5x^4-15x^3+4x^2+12x\]](https://www.cursomates.com/wp-content/ql-cache/quicklatex.com-d1a69fa8b8fc7ccff416c3d6d5085959_l3.png)
Con esto ya puedes deducir que si el polinomio no corta al eje ![]() no vas a poder encontrar raíces del mismo, y que el hecho de que una raíz sea doble significa que corta dos veces en el mismo punto al eje
no vas a poder encontrar raíces del mismo, y que el hecho de que una raíz sea doble significa que corta dos veces en el mismo punto al eje ![]() . Todo esto es un poco más técnico, pero como aproximación nos vale.
. Todo esto es un poco más técnico, pero como aproximación nos vale.
Teorema del resto
Mediante este teorema vamos a poder calcular el resto de una división de un polinomio ![]() entre un monomio de grado UNO
entre un monomio de grado UNO ![]() de una forma muy rápida y sencilla. El teorema dice lo siguiente:
de una forma muy rápida y sencilla. El teorema dice lo siguiente:

![]() un polinomio y sea
un polinomio y sea ![]() un monomio de grado UNO. El resto de la división de
un monomio de grado UNO. El resto de la división de ![]() es el valor numérico
es el valor numérico ![]()
Dos cuestiones muy muy importantes hay que recalcar aquí:
- Sólo se puede calcular el resto cuando divides por un monomio de grado UNO (te lo estoy poniendo todo el rato en mayúsculas). Es decir, si divides por
 ,
,  ,
,  , etc. Pero el teorema NO ES VÄLIDO si divides por
, etc. Pero el teorema NO ES VÄLIDO si divides por  o (
o ( por ejemplo. Si lo haces, tu profe que no te tiene manía te lo va a contar como mal, muy mal.
por ejemplo. Si lo haces, tu profe que no te tiene manía te lo va a contar como mal, muy mal. - Cuidado con los signos 🤦🏻♂️ Cuando divides al polinomio
 entre
entre  , calculas el valor numérico para
, calculas el valor numérico para  . Esto significa que TIENES QUE CAMBIAR EL SIGNO entre el término independiente del divisor (el numerito
. Esto significa que TIENES QUE CAMBIAR EL SIGNO entre el término independiente del divisor (el numerito  ) y cuando calculas el valor numérico del polinomio (aquí calculas
) y cuando calculas el valor numérico del polinomio (aquí calculas  .
.
Si volvemos a la tabla del principio, ¿puedes aventurar si habrá algunas divisiones exactas? ¿de qué polinomios entre que monomios? échale un vistazo 
Teorema del factor
El teorema del factor te permite buscar números candidatos a ser raíces del polinomio. El auténtico teorema del factor dice:

![]() una raíz de un polinomio
una raíz de un polinomio ![]() Entonces se verifica que
Entonces se verifica que ![]() es divisor de
es divisor de ![]() y
y ![]() es divisor de
es divisor de ![]() .
.
Sin embargo, en la ESO descafeinamos un poco este enunciado y lo expresamos así:

En el fondo estamos diciendo lo mismo, pero el auténtico teorema del factor es el primero.
De todas maneras aquí aparece un problema y es saber cuáles son los divisores de un número (en este caso el término independiente), pero esto ya te lo he explicado en otra entrada.
¿Cuántos factores va a tener un polinomio?
Esta es una pregunta muy interesante. Cuando factorizas números no puedes saber cuántos factores vas a encontrar. Por ejemplo, si factorizas ![]() sólo vas a encontrar el factor
sólo vas a encontrar el factor ![]() que aparece cuatro veces
que aparece cuatro veces ![]() sin embargo, para el
sin embargo, para el ![]() tendrás dos factores que son el
tendrás dos factores que son el ![]() y el
y el ![]() (
(![]() ) y con el
) y con el ![]() te habrás encontrado con un número primo.
te habrás encontrado con un número primo.
Si bien con números no tienes una forma de saber cuántos factores vas a encontrar, con polinomios sí. De hecho es un resultado tan importante que se llama Teorema Fundamental del Álgebra, y dice lo siguiente.
Teorema fundamental del álgebra

![]() , con coeficientes en el conjunto de números complejos, existen exactamente
, con coeficientes en el conjunto de números complejos, existen exactamente ![]() raíces, no forzosamente distintas
raíces, no forzosamente distintas
Tranquilo que te lo traduzco a lo que vas a ver en clase:
- Todo polinomio en una variable de grado
 (normalmente se suele decir que
(normalmente se suele decir que  , piensa por qué) significa que el polinomio será, al menos de la forma
, piensa por qué) significa que el polinomio será, al menos de la forma  que es un polinomio en una variable,
que es un polinomio en una variable,  , y que además tiene grado
, y que además tiene grado  . Como el grado tiene que ser mayor o igual que uno, también pueden ser, por ejemplo, los siguientes
. Como el grado tiene que ser mayor o igual que uno, también pueden ser, por ejemplo, los siguientes  ,
,  ,
,  etc. Creo que ya ves por donde vamos.
etc. Creo que ya ves por donde vamos. - Con coeficientes complejos: en la ESO no se ven números complejos y en bachillerato depende del curso en el que estés o de la rama que hayas elegido, así que en la ESO y bachillerato esta parte del enunciado podrías leerla como «con coeficiente reales», y significa que todos los coeficientes del polinomio son números reales. Y número real significa número real, no significa racional, entero o natural.
- Tiene exactamente
 raíces, no forzosamente distintas: Aquí aparece el concepto de multiplicidad del que hemos hablado antes. Pero puesto que antes hemos rebajado nuestras expectativas de números complejos a reales, debes seguir leyendo la siguiente sección.
raíces, no forzosamente distintas: Aquí aparece el concepto de multiplicidad del que hemos hablado antes. Pero puesto que antes hemos rebajado nuestras expectativas de números complejos a reales, debes seguir leyendo la siguiente sección.
Aplicación en clase del TFA
Fíjate que hemos descafeinado un poco el teorema: hemos dicho que vamos a buscar raíces reales en un polinomio de coeficientes reales (exigencias del guión en la educación secundaria 
Así pues, yo a mis alumnos les digo que si tenemos un polinomio de grado ![]() , como mucho podremos localizar
, como mucho podremos localizar ![]() raíces (acuérdate que raíz de un polinomio y factor de un polinomio están relacionados).
raíces (acuérdate que raíz de un polinomio y factor de un polinomio están relacionados).
Pero aún hay más. Debido a que los polinomios que se trabajan en educación secundaria tienen coeficientes reales y no complejos, las raíces complejas (de existir) van a pares es decir, una raíz compleja y su conjugada. Por lo tanto, piensa un poco y deducirás que si el grado del polinomio que estás estudiando es ![]() resulta que:
resulta que:
- Si
 es par podrás encontrar
es par podrás encontrar  raíces distintas. Dependiendo de las raíces complejas, pareadas, que no vas a poder calcular, y de alguna otra que métodos como el algoritmo de Ruffini no te va a permitir detectar, aunque sean raíces reales.
raíces distintas. Dependiendo de las raíces complejas, pareadas, que no vas a poder calcular, y de alguna otra que métodos como el algoritmo de Ruffini no te va a permitir detectar, aunque sean raíces reales. - Si
 es impar, podrás encontrar
es impar, podrás encontrar  raíces distintas. Igual que antes, habrá raíces complejas que no vas a poder calcular y algunas reales que se te pueden escapar porque careces de las herramientas para detectarlas.
raíces distintas. Igual que antes, habrá raíces complejas que no vas a poder calcular y algunas reales que se te pueden escapar porque careces de las herramientas para detectarlas.
Y todo esto nos permite saber cuántos factores vamos a poder localizar como máximo, lo cual está muy bien, porque si no supiéramos esto, ¿Cuándo podríamos parar de buscar?
Así que ya sabes, si tienes un polinomio de cuarto grado, como mucho encontrarás cuatro raíces distintas; si tiene grado siete, como mucho encontarras siete raíces distintas, y así sucesivamente.
¿Qué pasa con el coeficiente director?
Como sabes, el coeficiente director es el número que acompaña a la ![]() de mayor grado. Pues bien, debes tenerlo muy, pero que muy en cuenta cuando factorices un polinomio, puesto que NO TE PUEDES OLVIDAR DE ÉL.
de mayor grado. Pues bien, debes tenerlo muy, pero que muy en cuenta cuando factorices un polinomio, puesto que NO TE PUEDES OLVIDAR DE ÉL.
Vamos a ver algunos ejemplos.
Ejemplo 1
Vamos a factorizar el siguiente polinomio:
![]()
Según lo ves, dices: como mucho voy a encontrar siete raíces y eso lo sabes porque el grado de este polinomio es 7. Ahora, con paciencia lo factorizas y localizas que sus factores primos son:
 con multiplicidad 2.
con multiplicidad 2. con multiplicidad 1.
con multiplicidad 1. con multiplicidad 3.
con multiplicidad 3. con multiplicidad 1.
con multiplicidad 1.
Así, ya sabes que la factorización de este polinomio es:
![]()
Y con esto se acabó. Ya lo tienes.
No obstante, yo te aconsejo que compruebes que el grado del polinomio factorizado es el mismo que el grado del polinomio que te dan en el problema. Es una forma rápida de comprobar que no lo tienes mal.
Ejemplo 2
Vamos a factorizar uno de los polinomios con los que hemos estado trabajando al principio.
![]()
Si factorizas este polinomio obtienes que sus factores primos son: ![]() ,
, ![]() ,
, ![]() Cada uno con su grado de multiplicidad correspondiente. Puedes tener la tentación de factorizar así el polinomio
Cada uno con su grado de multiplicidad correspondiente. Puedes tener la tentación de factorizar así el polinomio
![]()

Así, lo correcto es decir que la factorización de ![]() es:
es:
![]()
Así que ya sabes, siempre debes empezar la factorización por el coeficiente director.
Ejemplo 3
Ahora te voy a volver un poco loco 
![]()
Si calculas los factores primos de este polinomio podrás comprobar que son: ![]() ,
, ![]() y
y ![]() cada uno con su multiplicidad correspondiente que ahora verás.
cada uno con su multiplicidad correspondiente que ahora verás.
Como resulta que te has leído el ejemplo anterior, ya no caes en la trampa y no factorizas el polinomio anterior como:
![]()
Porque has dicho, date, aquí hay un coeficiente director que es 3 y lo tengo que poner en algún sitio Así que decides factorizarlo como
![]()
¿Puedes por favor, desarrollar el producto anterior a ver qué te sale? Es un poco largo, pero hazlo antes de seguir leyendo.
Por favor, desarrolla el polinomio anterior antes de leer.
Desarróllalo.
No hagas trampas, que con papel y boli no vas a tardar mas de 4 o 5 minutos.
Bueno, vale, te lo digo, que no te veo con la intención de hacer muchas cuentas… si desarrollas el polinomio te queda:
![]()
Pero… ¡¡¡cómo!!! 
![]() tienes un factor que no sólo no tiene grado uno si no que además incluye ya el coeficiente director. Es el factor
tienes un factor que no sólo no tiene grado uno si no que además incluye ya el coeficiente director. Es el factor ![]() . Así que ten mucho cuidado no sea que llegando al final del ejercicio metas la pata
. Así que ten mucho cuidado no sea que llegando al final del ejercicio metas la pata 
¿Y cómo lo puedo saber? ¿Cómo sé si debo poner el coeficiente director o no? Muy fácil. haz un cálculo rápido y multiplica de cada uno de los factores que has hallado del polinomio, la ![]() de mayor grado. Así, para este ejemplo tienes:
de mayor grado. Así, para este ejemplo tienes:
![]()
Que resulta ser el primer término de nuestro polinomio problema. Esto significa que no debes multiplicarlo por el coeficiente director.
Te pongo esta idea recuadrada en verde
Sea ![]() , y sean
, y sean ![]() las raíces del polinomio con multiplicidad
las raíces del polinomio con multiplicidad ![]() . Entonces, la factorización de
. Entonces, la factorización de ![]() salvo el orden de los factores es:
salvo el orden de los factores es:
![]()
Pero si el polinomio tiene algún factor de grado distinto de 1 (esto es, alguna de las raíces del polinomio no es una raíz real si no compleja) o bien el coeficiente principal de alguno de los factores es distinto de un; puede ocurrir que ese factor ya incluya a ![]()
Y hasta aquí la entrada de hoy dedicada a la factorización de polinomios. En la siguiente entrada te diré cómo factorizar polinomios con la regla de Ruffini, que no es más que un algoritmo para dividir polinomios de forma muy rápida, sencilla y eficaz.

Si quieres contactar conmigo puedes hacerlo aquí
Si te gusta lo que hago y quieres invitarme a un café 
Vida de la entrada:
– 2020-11-12: Publicación.
–
Bibliografía
- Suprún, V. P.; 2011; Matemática para estudiantes preuniversitarios: Métodos no estándares para la resolucín de ecuacines y desigualdades. 350 problemas detalladamente resueltos; Ed. HAYKA-URSS; Moscú; ISBN: 978-5-369-00369-9 (edición en español)
- Suprún, V. P.; 2011; Matemática para estudiantes preuniversitarios: Problemas de alta dificultad. 300 problemas detalladamente resueltos; Ed. HAYKA-URSS; Moscú; ISBN: 978-5-396-00101-5 (edición en español)

 )
)



