▶ ➗ Racionalización de fracciones 💥

[latexpage]

Hola profemaniático, hoy te traigo malas noticias. Lamento decirte que tendrás que aprender a racionalizar fracciones tarde o temprano, así que mejor que aprendas ya y te olvides de otras preocupaciones. Lo vas a usar muchas, muchísimas veces, por ejemplo cuando estudies trigonometría y debas resolver ecuaciones trigonométicas; y en general cuando tengas que dar un resultado que sea una fracción y en el denominador haya un número real expresado como una raíz cuadrada.

Así que estás aquí porque no te parece nada racional que tengas que aprender a racionalizar fracciones Y más teniendo calculadora, y más teniendo ordenadores y más… bueno, no te preocupes. Antes tenía malas noticias, ahora tengo dos buenas:

• La racionalización no es un proceso tan complejo, sobre todo en la ESO y Bachillerato. 👍
• Para la racionalización de fracciones los algoritmos son muy sencillos. 👍👍

La racionalización de fracciones se empieza a ver en 4ESO. Esto es así porque antes se debe aprender a manejar las fracciones algebraicas, que formalmente se empiezan a estudiar en 3ESO.

Cuando empiezo a explicar este tema siempre empiezo realizando algunas divisiones muy sencillas como $17:5$ que den un decimal exacto y luego paso a divisiones donde el divisor sea un número con decimales, como por ejemplo $17: 5,23$ Lo que pretendo hacer ver a los alumnos es que cuando dividimos por un número decimal, calcular el cociente de la división implica conocer todas y cada una de las cifras que aparecen en la parte decimal del divisor. Piénsalo y verás como es verdad.

Y todo esto ¿para qué?😤 Sencillo, resulta que no se puede dividir por números irracionales tan fácilmente. Por ejemplo la siguiente división no la podríamos realizar a mano $1:\sqrt{2}$ Ya que si colocamos los números en el algoritmo obtenemos que:

$\begin{tabular}{cc}
1 & \hspace*{-4pt}\vline \hspace*{5pt} 1,4142135623730950488016887242096980785696718753769480731766797379\ldots \\\cline{2-2}
??& \text{¿cuál es el cociente si no conocemos el divisor exacto?}
\end{tabular}$

Y aún no hemos ni siquiera empezado a colocar el divisor para realizar la operación 😕

Sin embargo, si tenemos un número irracional y lo dividimos por otro siempre tenemos la oportunidad de parar ✋🏻 cuando queramos. Quiero decir que si queremos asegurarnos un error menor de $10^{-3}$, porque dicho error es asumible en nuestros cálculos, sabemos que tenemos que sacar 3 dígitos decimales y para ello sólo necesitamos unos pocos decimales del número irracional. Por ejemplo, si queremos dividir $\sqrt{2}:3$ con un error menor de $10^{-3}$ nos basta con hacer la siguiente operación.

$\begin{tabular}{lc}
1,4142\ldots & \hspace*{-30pt}\vline \hspace*{5pt}3 \\\cline{2-2}
\phantom{1,}21& 0,471\ldots\\
\phantom{1,4}04&\\
\phantom{1,41}\ddots&\\
\end{tabular}$

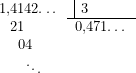
Lo interesante de esta división es que no necesitamos conocer el valor exacto de $\sqrt{2}$ para calcularlo, si no que nos basta con un valor aproximado tan bueno como queramos.

Pues de esto precisamente es de lo que trata esta entrada. De como poder dividir por algunos números irracionales sin necesidad de conocerlos en su totalidad, lo cual de manera práctica es imposible.

Por qué necesitamos racionalizar ⁉

Creo que esta pregunta ya te la he respondido antes. Pero ahora puedes hacer un ejercicio de imaginación. Imagínate que vives en algún momento antes de 1960. Los ordenadores no existen; no al menos, como los conocemos hoy, y mucho menos como ese electrodoméstico que aparece en casi todas las casas hoy en día. 💻

Así que para poder realizar operaciones como las siguientes necesitas conocer el algoritmo de la racionalización:

$$\frac{2}{\sqrt{3}}\qquad\qquad \frac{5}{2-\sqrt{5}}\qquad\qquad\frac{\sqrt{7}}{\sqrt{3}-1}$$

Ahora bien, no siempre es posible racionalizar y a veces es bastante más complicado poder racionalizar de lo que parece.

Por ejemplo, las siguientes fracciones no son fáciles de racionalizar con el método que te voy a decir dentro de un rato.

$$\frac{3}{\sqrt[3]{2}+1}\qquad \qquad\frac{2}{\pi}\qquad \qquad\frac{2}{3\pi \log 2}\qquad \qquad\frac{5}{\sqrt{2+\sqrt[3]{4}}}$$

Tranquilo, para estos casos hay otras técnicas. Quizá la más ingeniosa es la del uso de los logaritmos, pero en esto no vamos a entrar ahora. En esta entrada nos vamos a dedicar a racionalizar fracciones que te van a aparecen en 4ESO y durante el bachillerato. Nada más.

Lo importante es que te quede claro que hay ocasiones en las que es imprescindible racionalizar para poder continuar operando. Con esto te digo que lo que yo te voy a contar ahora no es un fin en sí mismo; a nadie le importa la racionalización de $\displaystyle \frac{4}{\sqrt{2}-3}$ ¿a nadie? bueno a nadie que no tenga que seguir haciendo cuentas con ese número y necesite dar un resultado lo más exacto posible. Puede ocurrir que ese número sea importante para el cálculo del espesor de un dique, el tamaño de un buque, el diámetro de un cable de alta tensión… y es ahí donde aparece la importancia de la racionalización.

Déjate de rollos. Quiero ver una racionalización.

Sí, tienes razón. Me he enrollado mucho y hasta ahora no hemos entrado al grano. Ahora te voy a explicar cómo racionalizar unas cuantas fracciones y espero que te sirvan para aprender al algoritmo.

El objetivo fundamental de la racionalización

El objetivo fundamental que debes perseguir cuando racionalizas es eliminar cualquier número irracional del denominador de la fracción (generalmente raíces o suma de raíces y números racionales). Así hay dos estrategias fundamentales:

• Completar la raíz.
• Utilizar los productos notables.

En el primer caso se trata de que el radicando de la raíz sea un cuadrado perfecto, cubo perfecto… según nos indique el índice de la raíz; para que podamos operarlo y así eliminar la raíz del denominador.

En el segundo caso, lo que iremos buscando será generalmente una suma por diferencia, que al igual que antes nos permita eliminar la raíz del denominador. En este caso la estrategia se basa en multiplicar por el conjugado del número que aparece en el denominador.

Además nunca debes perder de vista el hecho de que el valor del número debe ser el mismo antes y después de que tú hayas procedido a la racionalización. Esto se consigue multiplicando por UNO, pero mejor te lo explico en los primeros ejemplos para no liarte.

¿Conjugado no es un tiempo verbal?

No. Tranquilo, cuando se habla en matemáticas de conjugado no estamos hablando de verbos si no de números. Cuando estudies los números complejos ya tendrás tiempo de pelearte más a fondo y saber qué es un conjugado con más exactitud; pero de momento te los voy a presentar.

Cuando tienes un número como $\sqrt{2}+3$ su conjugado es el mismo número pero cambiando la suma por una resta, es decir $\sqrt{2}-3$. Igualmente si necesitas racionalizar y el número que te da problemas es $\sqrt{5}-1$ su conjugado será el mismo número pero cambiando la resta por una suma, es decir: $\sqrt{5}+1$. Date cuenta que el hecho de ser conjugado de se puede ver en ambas direcciones; o sea que $\sqrt{6}-\sqrt{8}$ es el conjugado de $\sqrt{6}+\sqrt{8}$; pero también al revés, $\sqrt{6}+\sqrt{8}$ es el conjugado de $\sqrt{6}-\sqrt{8}$. Se dice que es una relación simétrica, pero no entraremos en ese jardín.

Aquí te dejo una serie de números y sus conjugados.

Empieza la racionalización

A continuación te voy a poner unos pocos ejemplos de cada tipo de ejercicio que te puedes encontrar de racionalización. Debes entender que cuando hablo de sumas igualmente estoy indicando restas. Ya sabes aquello de que restar es sumar el opuesto de un número.

Racionalización con una raíz en el denominador

Cuando racionalizas una fracción con una raíz en el denominador, lo que debes hacer es completar la raíz. El signo de la fracción no va a jugar un papel relevante en el proceso de racionalización, pero debes tenerlo en cuenta pues el signo de la fracción es el que es y no lo puedes quitar alegremente.

Ejemplo 1

Vamos a racionalizar $\displaystyle \frac{3}{\sqrt{2}}$ En este caso nos fijamos en el denominador de la fracción y vemos que es una raíz cuadrada. Para completarla debemos multiplicar el denominador por $\sqrt{2}$ pero si simplemente hacemos esto, lo que conseguiremos es calcular otro número distinto. Para que esto no ocurra lo que hacemos es multiplicar el numerador también por $\sqrt{2}$. Así que procedemos de esta manera.

$\displaystyle \frac{3}{\sqrt{2}}\cdot \color{red} \frac{\sqrt{2}}{\sqrt{2}}$

Con esto conseguimos dos cosas:

• El número está multiplicado por UNO, por lo que su valor no cambia.
• Cuando multipliques, el denominador va a quedarte $\sqrt{2}\sqrt{2}=2$ con lo que el número irracional va a desaparecer de allí.

Continuamos:

$\displaystyle \frac{3}{\sqrt{2}}\cdot \color{red} \frac{\sqrt{2}}{\sqrt{2}}\color{red}\color{black}= \frac{3\sqrt{2}}{2}$

Como esta última fracción no se puede simplificar, significa que hemos terminado el proceso. Así pues, la racionalización de $\displaystyle \frac{3}{\sqrt{2}}$ es $\displaystyle \frac{3\sqrt{2}}{2}}$

$$\displaystyle \frac{3}{\sqrt{2}}=\displaystyle \frac{3\sqrt{2}}{2}}$$

Ejemplo 2

Ahora vamos a racionalizar la siguiente fracción:

$\displaystyle \frac{-5}{\sqrt[3]{4}}$

En este caso nos debemos fijar en varias cosas:

• El signo menos de la fracción no nos va a influir en el resultado, así que no le tengas miedo. Toca operar con el denominador.
• La raíz del denominador es cúbica, por lo que debemos completar un cubo en vez de un cuadrado para poder racionalizar.
• Por último, fíjate en el radicando, es un $4=2^2$ por lo que, en realidad la racionalización la podremos hacer cuando completemos el cubo de 2.

Vamos a seguir:

$\displaystyle \frac{-5}{\sqrt[3]{4}}=\frac{-5}{\sqrt[3]{2^2}}\cdot \color{red} \frac{\sqrt[3]{2}}{\sqrt[3]{2}}$

Cuando multiplico y divido por $\sqrt[3]{2}$ lo que consigo son dos cosas:

• Multiplico por uno, con lo que el valor del número calculado no va a cambiar.
• Completo el cubo en el denominador, lo que me permite eliminar el número irracional de denominador.

Seguimos:

$\displaystyle\frac{-5}{\sqrt[3]{2^2}}\cdot \color{red} \frac{\sqrt[3]{2}}{\sqrt[3]{2}}\color{black}=\frac{-5\sqrt[3]{2} }{\sqrt[3]{2^3}}=\frac{-5\sqrt[3]{2} }{2}$

Y como esta última fracción es irreducible, ya hemos terminado la racionalización.

Ejemplo 3

Vamos a hacer el último ejemplo de racionalización con una única raíz en el denominador:

$\displaystyle \frac{4}{\sqrt[4]{2}}$

En este caso, para racionalizar, debemos completar una raíz cuarta. Pero esto ya lo hemos hecho antes, así que vamos a ir un poco más rápido:

$\displaystyle \frac{4}{\sqrt[4]{2}}\cdot \color{red}\frac{\sqrt[4]{2^3}}{\sqrt[4]{2^3}}\color{black}=\frac{4\sqrt[4]{8}}{2}=\color{red}2\sqrt[4]{8}$

Como ves en este ejemplo ocurren dos cosas que aún no habíamos visto:

• Al final la fracción se puede simplificar.
• El resultado final no tiene por qué ser una fracción.

Racionalización con suma de un número y una raíz en el denominador.

En los ejemplos anteriores, tenemos que el denominador siempre es una raíz que está sola, así que la mayor dificultad era ver como completar el radicando para que fuese un cuadrado, un cubo, una cuarta potencia…

Ahora la cosa cambia, en este caso el denominador está constituido por un número (normalmente será entero) y una raíz. Para poder hacer esta racionalización debes utilizar los números conjugados de los que te he hablado antes y los productos notables, en concreto suma por diferencia.

Ejemplo 1

Veamos como racionalizar la siguiente

$\displaystyle \frac{2}{3+\sqrt{2}}$

Igual que siempre lo que debemos hacer es buscar un número que multiplique numerador y denominador, y que además elimine la raíz del denominador. Para ello usamos el conjugado del denominador que es $3-\sqrt{2}$:

$\displaystyle \frac{2}{3+\sqrt{2}} \cdot \color{red} \frac{3-\sqrt{2}}{3-\sqrt{2}}$

Y ahora solo tienes que multiplicar, con cuidado de no confundirte, eso sí.

$\displaystyle \frac{2}{3+\sqrt{2}} \cdot \color{red} \frac{3-\sqrt{2}}{3-\sqrt{2}}\color{black}= \frac{6-2\sqrt{2}}{9-2}=\frac{6-2\sqrt{2}}{7}$

Y debes observar que esa fracción es irreducible, así pues ya has terminado la racionalización.

Ejemplo 2

Considera ahora la siguiente

$\displaystyle \frac{2}{\sqrt{5}+2}$

Hacemos lo mismo que antes. Calculamos el conjugado del denominador, multiplicamos …

$\displaystyle \frac{2}{\sqrt{5}+2}\cdot \color{red} \frac{\sqrt{5}-2}{\sqrt{5}-2}\color{black}=\frac{2\sqrt{5}-4}{5-4}=2\sqrt{5}-4$

Como ves, en este caso el resultado final de esta racionalización no es siquiera una fracción,

Ejemplo 3

Vamos con el último ejemplo de este tipo:

$\displaystyle \frac{12}{4+\sqrt{8}}$

¿Adivinas qué hay que hacer?… Exacto, buscar el conjugado del denominador y….

$\displaystyle \frac{12}{4+\sqrt{8}}\cdot \color{red}\frac{4-\sqrt{8}}{4-\sqrt{8}}\color{black}=\frac{12\left(4-\sqrt{8}\right)}{8}=\frac{3}{2}\left(4-\sqrt{8}\right)=6-\frac{3}{2}\sqrt{8}$

Aquí los cálculos son un poco más largos porque la simplificación de la fracción no es inmediata, pero ves que con un poco de paciencia se resuelve sin problemas.

Racionalización con suma de dos raíces en el denominador.

Si has llegado hasta aquí te puedes considerar todo un experto en racionalización. Lo que vamos a hacer ahora es ir un paso más allá poniendo dos raíces en el denominador, pero tranquilo, el proceso es el mismo. Debes multiplicar por el conjungado y esas cosas que ya dominas:

Ejemplo 1

En este caso nos piden racionalizar lo siguiente:

$\displaystyle\frac{3}{\sqrt{2}-\sqrt{3}}$

Para ello multiplicamos por el conjugado del denominador y operamos:

$\displaystyle\frac{3}{\sqrt{2}-\sqrt{3}}\cdot \color{red}\frac{\sqrt{2}+\sqrt{3}}{\sqrt{2}+\sqrt{3}}\color{black}=\frac{3\sqrt{2}+3\sqrt{3}}{-1}=-3\sqrt{2}-3\sqrt{3}$

Y esta es la solución de esta racionalización.

Ejemplo 2

Vamos a complicar ahora un pelín el numerador, que todavía no ha aparecido ninguna raíz allí. Pero ahora ya te lo escribo todo directamente.

$\displaystyle\frac{5\sqrt{3}}{\sqrt{3}+\sqrt{2}}\cdot\color{red}\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}-\sqrt{2}}\color{black}=\frac{5\cdot 3-5\sqrt{2}}{1}=15-5\sqrt{2}$

Ejemplo 3

Y ahora vamos con el último, donde aparece una suma de raícesn en el numerador y otra en el denominador ¡¡TOOOMAAA YAAA!! Pero siempre, el conjugado del denominador.

$\displaystyle\frac{4\sqrt{2}-2\sqrt{3}}{\sqrt{2}+\sqrt{3}}\cdot \color{red}\frac{\sqrt{2}+\sqrt{3}}{\sqrt{2}+\sqrt{3}}\color{black} = \frac{4\sqrt{2}\sqrt{2}-4\sqrt{2}\sqrt{3}-2\sqrt{3}\sqrt{2}+2\sqrt{3}\sqrt{3}}{-1}=…$

Y la solución de todo lo anterior es

$$6\sqrt{6}-14$$

En definitiva

Como ves la racionalización de fracciones no es una técnica difícil. Personalmente creo que operar con logaritmos, por ejemplo un cambio de base; o resolver una inecuación, puede llegar a ser más complejo que una racionalización de las que te encuentras en la ESO o bachillerato en España.

A pesar de todo te dejo aquí un esquema que te pueda servir para enfrentarte a una racionaliación en el futuro. ¡¡¡Mucha suerte‼‼

Si quieres contactar conmigo puedes hacerlo aquí

Si te gusta lo que hago y quieres invitarme a un café ¡¡te doy las gracias por adelantado!!