▶ 👍 Logaritmos ¿qué son? ¿se usan? 🥇

Cuando debes realizar operaciones aritméticas, es muy importante no confundirte. Además, hay operaciones que son más sencillas que otras.

Por ejemplo, tomemos los números $1567$ y $4587$ podemos sumarlos y restarlos con relativa facilidad:

$\text{\begin{tabular}{ccccc} &1&5&6&7\\ +&4&5&8&7\\\hline \phantom{\Huge H} &6&1&5&4\end{tabular} }$

$\text{ \begin{tabular}{ccccc} &4&5&8&7\\ -&1&5&6&7\\\hline &3&0&2&0 \end{tabular} }$

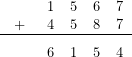
Pero si lo que necesitamos es multiplicarlos o dividirlos, la cuestión se vuelve más peliaguda. Para multiplicarlos, mediante el algoritmo que conocemos, necesitamos ser muy cautos: Todos los dígitos se van a acabar multiplicando por todos, pero debemos ser muy cuidadosos con su colocación para no cometer errores.

Lo mismo podemos decir de la división. El algoritmo (cómo se hace) no es difícil, pero es fácil confundirse y arrastrar equivocaciones, lo cual implica pérdida de tiempo y esfuerzo. Eso produce que con números largos, las operaciones dejen de ser triviales.

Observa el algoritmo de la división y multiplicación para estos dos números, y comprueba por ti mismo que aunque de ejecución sencilla, es muy, pero que muy fácil, confundirse:

$\text{ \begin{tabular}{ccccccc} &&&1 &5 &6 &7 \\ & &· &4 &5 &8 &7 \\\hline &&1&0&9&6&9 \\ &1&2&5&3&6& \\ &7&8&3&5&& \\ 6&2&6&8&&& \\\hline 7&2&8&7&8&2&9 \end{tabular}}$

$\text{ \begin{tabular}{ccc ccc l} 4&5&8&7&&& \vline 1567 \\\cline{7-7} 1&4&5&3&0&&2,92\ldots\\ &&4&2&7&0\\ &&1&1&3&6\\ &&&&\vdots \end{tabular}}$

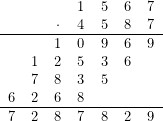
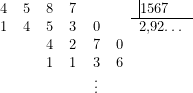
Estarás conmigo en que es mucho más fácil sumar o restar que multiplicar o dividir. Pues bien, la ventaja ENORME que tienen los logaritmos es que van a transformar productos en sumas y las divisiones se convierten en restas. Tan sólo necesitamos tener una buena tabla que nos permita traducir un número a su logaritmo y viceversa; hoy en día esa tabla está integrada en las calculadoras.

De hecho, la invención de los logaritmos fue un paso tan importante, que el matemático francés Pierre Simón Laplace dijo de ellos lo siguiente:

Reduce a unos pocos días la labor de muchos meses, dobla la vida del astrónomo y le ahorra errores y disgustos.
Pierre Simón de Laplace (Matemático francés, 1749-1825)

¿Qué es un logaritmo? Definición.

En 4 ESO se definen los logaritmos poniéndolos en relación con las potencias. Así decimos que :

$\log_ab=c \quad \Longleftrightarrow \quad a^c=b$

El número $a$ se denomina base del logaritmo, y en principio puede ser cualquiera, con la única condición de que sea mayor que 0 y distinta de 1 (ahora veremos que suelen ser $10$ y $e$ ).
El número $b$ es el «logaritmando» (no sé si esta palabra existe), pero vamos, es el número al que voy a calcular el logartimo.
$\log$ es un operador, esto es, no tiene ningún sentido a no ser que vaya acompañado de sus números $a$ y $b$ respectivos. Hay otros operadores que ya conoces, como $+$ o $-$ , así que piensa que al igual que $+$ por sí mismo no significa nada a no ser que vaya acompañado de números como en $4+8$ , no tiene ningún sentido poner $\log$ o $\log_3$ ; lo que tiene sentido es $\log_2 7$ , $\log_9 23$ …
$\log_ab$ ES un número real que será más grande o más pequeño dependiendo del valor de $a$ y de $b$ . De hecho $\log_a b$ puede ser tanto negativo como positivo, y salvo que $b$ sea una potencia entera de $a$ , el número $\log_ab$ será un número irracional.

Como podrás imaginarte, la función logaritmo (y la función exponencial, ya que ambas están asociadas) se define de una manera mucho más técnica (si te interesa la definición «auténtica» puedes echar un vistazo al libro de Linés que te dejo en la bibliografía), pero la definición que te he dado, nos permite avanzar en el conocimiento de la herramienta sin necesidad de diatribas matemáticas.

A partir de esta definición tu profe, que no te tiene manía, te habrá explicado algunos ejemplos como los que te pongo a continuación:

$\log_39=2\Leftrightarrow 3^2=9$
$\log_5125=3\Leftrightarrow 5^3=125$

$\log_4256=4\Leftrightarrow 4^4=256$
$\log_28=3\Leftrightarrow 2^3=8$

$\log_{10}100=2\Leftrightarrow 10^2=100$
$\log_{10}1000=3\Leftrightarrow 10^3=1000$

Supongo que no te extrañará si te digo que tu día a día con los logaritmos no se va reducir a estos ejemplos triviales y sin mayor trascendencia. En clase te los habrán enseñado para que interiorices completamente qué es un logaritmo. Es muy importante que estos ejemplos los manejes casi con los ojos cerrados, pero con lo que trabajarás será algo más complicado; no obstante puedo asegurarte que el mundo de los logaritmos te va a resultar muy útil para resolver problemas de lo mas variopintos: radioactividad, expansión de una enfermedad, crecimiento bacteriano, matemática financiera, crecimiento de la madera en un bosque, intensidad de los terremotos…

Vale, genial. Pero ¿Qué bases se usan?

Pues es una muy buena pregunta. Porque hasta no hace muchos años los logaritmos se calculaban a mano y luego se tabulaban para poder tenerlos disponibles si se necesitaban.

Tabla de los logaritmos de Briggs o vulgares.

En la imagen anterior puedes ver lo que te comentaba un poco más arriba. En ella aparecen los logaritmos en base 10 ªhasta 399, pero el libro de donde lo he sacado tiene todos los logaritmos, en base 10, hasta el número 20000. De esta manera, si quieres saber cuánto es, por ejemplo, $\log_{10} 90$ tan sólo tienes que buscarlo en la tabla: $\log_{10} 90=1,954243$ .

Todos estos cálculos puedes imaginártelos aburridos y tediosos, además implican aproximar y redondear, ya que el valor correcto es imposible de escribir. Como buenos números irracionales, los logaritmos salvo las potencias de las bases, tienen infinitas cifras decimales sin patrón reconocible. Por ejemplo:

$\log_{10}90=1,954242509439324874590055806510230618400…$

Ya que nuestro sistema de numeración está basado en base 10, no es de extrañar que una de las bases más comunes que se usan en los logaritmos sea la base 10. De hecho cuando se escriben logaritmos y no se especifica la base, se supone que la base es 10. Así, por convenio realizamos la siguiente identificación: $\log 35=\log_{10}35$ .

Otra base muy utilizada es el número $e$ . La definición de este número y qué es, te lo contaré en otra entrada, pero de momento quédate conque el número $e$ es la base de los logaritmos neperianos. También ocurre que es tan importante que cuando queremos decir que estamos calculando un logaritmo en la base $e$ escribimos $\ln$ en lugar de $\log$ . Por lo que cuando veas escrito $\ln 10$ tienes que interpretar que la base utilizada es el número $e$ ; como en este ejemplo: $\ln 10=\log_e 10$

No obstante, debes tener cuidado sobre cómo se nombran los logaritmos porque hay autores que a los logaritmos neperianos (que yo te he dicho que escribimos como $\ln$ ) los denominan $\log$ o incluso simplemente $L$ . Yo te he contado lo más común, pero si algún día tienes que leer algo sobre logaritmos, lo primero que debes hacer es investigar cómo van a nombrar los distintos logaritmos para no confundirte con los resultados.

Lo siguiente que te habrán explicado son las propiedades de los logaritmos, que es imprescindible que conozcas, comprendas y emplees correctamente.

Propiedades de los logaritmos.

Como ya te he dicho antes, las propiedades que te voy a nombrar ahora las debes conocer y manejar con soltura. Tan sólo te las voy a enunciar, no te las voy a deducir, aunque es sencillo partiendo de la definición. ¡¡Vamos con ellas!!

Logaritmo de un producto

El logaritmo de un producto, es la suma de logaritmos:
$\log_a(B\cdot C)=\log_a B+\log_aC$

Logaritmo de un cociente

El logaritmo de un cociente, es la resta de logaritmos:
$\displaystyle \log_a\left(\frac{B}{ C}\right)=\log_a B-\log_aC$

Es importante, aquí, que veas cómo es el denominador de la fracción quien se convierte en el sustraendo (el número que resta, vamos ).

Logaritmo de una potencia

El logaritmo de una potencia es el producto del exponente por el logaritmo de la base de la potencia:
$\log_a(B^C)=C\cdot \log_a B$

Como una potencia, $B^C$ , no es más que un producto de $B$ repetido $C$ veces; y como cada producto es una suma; al final hay $C$ sumandos que son $\log_aB$

Logaritmo de la base

El logaritmo de la base siempre es la unidad.
$\log_a a=1$

Piensa que si tienes $\log_a a=p$ la pregunta que te debes hacer es ¿qué número debe ser $p$ para que $a^p=a$ ? Lógicamente debe ser 1.

Logaritmo de 1

El logaritmo de 1 es siempre 0. ¡¡En cualquier base!!
$\log_a 1=0$

Igual que antes, si tienes $\log_a 1=p$ debes pensar ¿A qué número debo elevar $a$ para que me dé 1?

Fórmula del cambio de base

A veces es necesario calcular logaritmos en bases «raras», que no aparecen tabuladas en ningún sitio. Por lo que, al final, debemos referirlas a aquellas bases que sí sabemos manejar.

Imagínate que te piden el siguiente logaritmo: $\log_\pi 10$ ¡¡Un logaritmo en base $\pi$ !! Pero no te preocupes, que podría ser peor, como por ejemplo éste $\log_{2^\pi}\sqrt{7}$ . Claramente, si ves esto, lo más fácil es que te entren ganas de salir corriendo y olvidarte del tema. Pero no desesperes, para eso tenemos la fórmula del cambio de base, te lo voy a referir para base 10:

Para calcular un logaritmo en una base distinta dividimos el logaritmo del número entre el logaritmo de la base.
$log_a b=\displaystyle \frac{\log_{10} b}{\log_{10} a}$

Logaritmo de 0

No existe el logaritmo de 0. ¡¡En ninguna base!!

Esta peculiaridad te la he puesto como una propiedad, aunque en realidad no es ninguna propiedad. Pero me interesa que te quede claro, porque durante todos los años que llevo dando clase siempre hay alguien que comete este error.

Vamos a partir de la definición de logartimo: $\log_ab=c \Longleftrightarrow a^c=b$ pues la pregunta que debes hacerte es la siguiente:

Si $a\neq0$ es una base de una potencia (supongamos que $a>0$ , para facilitar la deducción), ¿cuál debe ser el exponente al que lo debo elevar, $b$ , para que la potencia $a^b=0$ ?

Puedes pensar durante un rato, pero al final te vas a dar cuenta que no existe ningún número $b$ tal que $a^b=0$ . Por lo tanto, espero que te quede claro:

No existe el logaritmo de 0. ¡¡En ninguna base!!

Si quieres, lo más adecuado es que digas que $b=-\infty$ pero eso en sí tampoco es un número real y en 1 Bachillerato ya tendrás tiempo para conocer el infinito y pelearte con él.

Ejemplos

A continuación te voy a poner algunos ejemplos de uso de los logaritmos. Debes tener en cuenta que en clase, tu profesor te propondrá otros parecidos. Al final de lo que se trata es de hacer ejercicios para tener soltura en el manejo de los logaritmos.

Todos los ejercicios que vas a ver aquí se resuelven aplicando directamente la definición o bien las propiedades de los logartimos. Si necesitas algún número en concreto puedes recurrir a la tabla que te he señalado antes.

Como truco general, si debes o tienes que descomponer un número para sacar su logaritmo, es muy interesante que itentes hallar potencias de la base en la que trabajas, porque de esa manera los cálculos se simplifican.

Por ejemplo $\log 25600$ . En este caso, lo que debes intentar hacer es factorizar el número 25600 donde te aparezcan potencias de 10. De esta manera tienes $\log 25600=\log (256\cdot 100)$ y se simplifica mucho los cálculos:

$\log 25600=\log (256\cdot 100)=\log 256+\log 100=2,408240+2=4,408240$

Si hallas la factorización canónica de 25600, es posible que las cuentas se enrevesen un pelín:

$\log 25600=\log (2^{10}\cdot 5^2)=10 \log 2 +2\log 5=10\cdot 0,301030+2\cdot 0,698970 =4,408240$

Como ves el resultado es el mismo, pero es más cómodo calcularlo de la primera forma.

Productos y logaritmos

1️⃣ $\displaystyle \log_3\left(27\cdot 81\right)=\log_3 27+\log_3 81=3+4=7$ Observa que $27\cdot 81=2187=3^7$

2️⃣ $\displaystyle \log_5\left(25\cdot 5\right)=\log_5 25+\log_ 5 5=2+1=3$ Ten en cuenta que $25\cdot 5=125=5^3$

3️⃣ $\displaystyle \log \left(10\cdot 20\right)=\log200=\log 2+ \log 100=0,301030+2=2,301030$

4️⃣ $\displaystyle \log\left(27\cdot 81\right)=\log 2187=\log (3\cdot3\cdot3\cdot3\cdot3\cdot3\cdot3) =\log 3+\log 3+\log 3+\log 3+\log 3+\log 3+\log 3=3,339849$

5️⃣ $\displaystyle \log\left(525)=log(25\cdot 21)=\log 25+\log 21=1,397940+1.322219=2,720159$

6️⃣ $\displaystyle \log\left(450)=\log(45\cdot 10)=\log 45 +\log 10=1,653213+1=2,653213$

7️⃣ $\displaystyle \log\left(1240)=\log( 124\cdot 10)=\log 124+\log 10=1,093422+1=2,093422$

8️⃣ $\displaystyle \log\left(3500\right)=\log 35+2=3,544068$

En este último ejemplo me he saltado algunos pasos porque los dos ceros de 3500 cuando tomas logaritmos son $\log 100=2$

Cocientes y logaritmos

Igual que con los productos, estos ejercicios son pura rutina. Debes practicarlos hasta que puedas verlos a ojo (no tanto el resultado, como el qué va a ocurrir)

1️⃣ $\displaystyle \log_3 \left(\frac{27}{81}\right)=\log27 - \log81 = 3-4=-1$ Los logaritmos pueden ser números negativos.

2️⃣ $\displaystyle \log \left(\frac{100}{37}\right)=\log100 - \log37 =2-1,568202=0,431798$

3️⃣ $\displaystyle \log \left(\frac{37}{100}\right)=\log37 - \log 100=1,568202-2=-0,431798$

Compara esta línea con la anterior ¿Qué conclusiones podrías sacar?

4️⃣ $\displaystyle \log \left(\frac{1}{23}\right)=\log 1- \log23 =0-1,361728=-1,361728$

5️⃣ $\displaystyle \log \left(\frac{19}{14}\right)=\log 19- \log14 =1,278754-1,146128=0,132626$

6️⃣ $\displaystyle \log 4,9= \log \left(\frac{49}{10}\right)=\log49 - \log10 =1,690196-1=0,690196$

Potencias y logaritmos

Las potencias de exponente entero y las multiplicaciones están muy ligadas. Lo que es un poco más difícil de ver son los exponentes negativos y decimales.

1️⃣ $\displaystyle \log 4^3=3\log 4=1,806180$

2️⃣ $\displaystyle \log 7^6=6\log 7=5,070588$

3️⃣ $\displaystyle \log 123^{3,12}=3,12\log 123=6,52050339$

4️⃣ $\displaystyle \log 4^{-3}=-3\log 4=-3\cdot 0,602060=-1,806180$

5️⃣ $\displaystyle \log 11^{-3}=-3\log =-3\cdot 1,041393=-3,124178$

6️⃣ $\displaystyle \log 0,25=\log 2^{-2}=-2\log 2=-0,602060$

7️⃣ $\displaystyle \log 0,25=\log\frac{1}{4}=\log 1-\log 4=0-0,602060=-0,602060$

Compara estas dos últimas líneas. ¿Qué conclusiones puedes obtener?

8️⃣ $\displaystyle \log 18^{-15}=-15\log 18=-18,829088$

9️⃣ $\displaystyle \log \sqrt{10}= \frac{1}{2}\log 10=\frac{1}{2}=0,5$

🔟 $\displaystyle \log\sqrt[5]{10}=\log 10^{1/5}=\frac{1}{5}\log 10=0,2$ El índice de una raíz no indica más que un exponente fraccionario del radicando.

Te voy a poner un último ejemplo algo desquiciante, para que puedas ver la potencia de los logaritmos:

💥

$\displaystyle \log\sqrt[\pi]{35011}=\frac{1}{\pi}\cdot \log(35011)=\frac{1}{\pi}\cdot\log (223\cdot 157)=\frac{1}{\pi}\cdot (\log 223+\log 157)=\frac{1}{\pi}\cdot(2,348305+2,195900)=1,446465$

Este es un ejemplo muy loco, pero te lo pongo porque me interesa contarte algo a continuación.

Imagínate que un día necesitas calcular una raíz cuadrada mostruosa como la anterior: $\displaystyle \sqrt[\pi]{35011}$ ¿Por dónde empezarías? porque, incluso con una calculadora, no es un ejercicio fácil. En este caso lo más sencillo, rápido, eficaz y seguro es utilizar logaritmos de la siguiente manera:

Lo primero que hago es llamar $A$ a mi raíz a calcular:

$A=\sqrt[\pi]{35011}$

Tomando logaritmos en ambos lados obtengo:

$\log A=\log\sqrt[\pi]{35011}=\ldots=1,446465$

Que efectivamente no es la solución. Pero ahora estarás de acuerdo conmigo, que estamos muy cerca. Simple y llanamente, debemos deshacer los logaritmos aplicando directamente la definición.

$\log A=1,446465\quad \Longrightarrow \quad A=10^{1,446465}=27,955378$

Así pues, la solución pedida es:

$A=\sqrt[\pi]{35011}=27,955378$

Yo el último paso lo he realizado con una calculadora, pero si quieres puedes intentar buscar en la tabla el número $1, 446465$ y ver de qué número es el logaritmo. Verás que es un número que tiene que estar entre 27 y 28, y para calcularlo te basta una interpolación sencilla (incluso una regla de tres).

Cambios de base

Vamos a usar la tabla de los logaritmos que aparece en la fotografía anterior para calcular alguno de ellos. Los resultados te los voy a dar con cuatro decimales correctamente redondeados.

1️⃣ $\displaystyle \log_3 10=\frac{\log 10}{\log 3}=\frac{1}{0,477121}=2,0959$

2️⃣ $\displaystyle \log_5 13=\frac{\log 13}{\log5}=\frac{1,113943}{0,698970}=1,593693$

3️⃣ $\displaystyle \log_{\pi} 11=$ {Vamos a redondear $\pi= 3,1416$ } $\displaystyle=\frac{\log11}{\log 3,1416}=\frac{1,041393}{0,495171}=2,103098$

Un uso curioso de los logaritmos.

Lo que viene a continuación no es algo que se cuente en clase. Yo nunca lo he hecho, y dudo que nadie lo haga. Pero es una aplicación, cuando menos curiosa, de los logaritmos.

Sin calcular el número, ¿me puedes decir cuántas cifras tiene $3^4$ ?, ¿y $2^{10}$ ? ¿y $7^{10}$ ? ¿y $2020^{2021}$ ? Ten en cuenta que no te pido que calcules qué número es, sólo te pido el número de dígitos. Por ejemplo: $3^4=81$ , $2^{10}=1024$ , $7^{10}=282475249$ ; pero yo no te pido eso, te pido que me digas cuántos dígitos tiene cada uno.

¿Cuántos dígitos tiene el número $2020^{2020}$ ?

Para llegar a responder a esta pregunta vamos a utilizar los logaritmos. Lógico. Es una entrada sobre logartimos… Sin embargo, antes de responder, examinemos qué relación tienen las potencias de 10 y sus logaritmos:

$\log 1=0$
$\log 10=1$
$\log 100=2$
$\log 1000=3$
$\log 10000=4$
$\log 100000=5$
$\log 1000000=6$
$\log 10000000=7$

Esto significa lo siguiente:

Todos los números que entran dentro del intervalo $(0,10)$ se escriben con un único dígito y poseen un logaritmo que es $0,\ldots$
Todos los números que entran dentro del intervalo $[10,100)$ se escriben con dos dígitos y poseen un logaritmo que es $1,\ldots$
Todos los números que entran dentro del intervalo $[100, 1000)$ se escriben con tres dígitos y poseen un logaritmo que es $2,\ldots$
Todos los números que entran dentro del intervalo $[1000, 10000)$ se escriben con cuatro dígitos y poseen un logaritmo que es $3,\ldots$

Y así podríamos seguir para todas y cada una de las potencias de 10; de forma que la parte entera del logaritmo del número, si le sumo una unidad, nos da el número de dígitos necesario para escribir un determinado número.

Por tanto:

Si quiero saber cuántos dígitos voy a necesitar para escribir un determinado número, simplemente debo hallar su logaritmo, tomo su parte entera, sumo una unidad, y ése será el número de dígitos necesario para escribir dicho número.

Ejemplo preliminar: ¿cuántos dígitos necesito para escribir $2^{30}$ ?

Para que lo tengas presente, te diré que $2^{30}=1\, 073\, 741\, 824$ es decir, es un número de 10 dígitos. Vamos a ver cómo llegamos a este resultado a través de los logaritmos.

En primer lugar, podemos plantear lo siguiente $2^{30}=N$ . Puesto que en principio no conozco el número, lo llamo $N$ . Si yo ahora tomo logaritmos puedo discurrir de la siguiente manera:

$\log N=\log 2^{30}=30\log 2=30\cdot 0,30103=9,0309$
Por lo tanto, la parte entera del logaritmo es $9$ (si lo quieres escribir de manera más formal deberías escribir $E[\log 2^{30}]=9$ )
Si a esa parte entera le sumo uno, obtengo 10.
Por lo tanto, 10 es el número de dígitos necesario para escribir $2^{30}$

Otro ejemplo: ¿cuántos dígitos necesitas para escribir $11^{22}$ ?

Seguimos el mismo camino que en el ejemplo anterior. En primer lugar llamo $M$ a mi número:

$11^{22}=N$

Y ahora simplemente tomo logaritmos, igual que antes:

$\log M=\log 11^{22}=22\cdot \log 11=22\cdot 1,04139=22,9106$
Me fijo en la parte entera del número anterior: 22
Sumo una unidad al número anterior: 23
Por lo que acabo de hallar cuántos dígitos necesito para escribir $11^{22}$ . Necesito un total de 23 dígitos.

Vamos ahora con el ejemplo que te he puesto al principio de este apartado: ¿cuántos dígitos tiene el número $2020^{2021}$ ?

Número de dígitos de $2020^{2021}$

Vamos a hacer exactamente lo mismo que antes, pero fijándonos en la tabla de logaritmos que te he dejado en la fotografía anterior:

Llamo $A=2020^{2021}$ y ahora tomo logaritmos.
$\log A=\log 2020^{2021}=2021\cdot \log 2020$ Y puesto que en la tabla de logaritmos no aparece cuanto es $\log 2020$ tengo que aplicar algunas de las propiedades de los logaritmos.

$\log 2020= \log\left( 10\cdot 202\right)\log \left(2\cdot 10\cdot 101\right)=\log 2+ \log 10+\log101= 0,30103+1+2,00432= 3,134423$
Acabo de calcular $\log 2020=3,134423$ . Ahora voy a calcular $\log 2020^{2021}$ que dejé pendiente en el paso anterior.

$\log 2020^{2021}=2021\cdot \log 2020=2021\cdot 3,134423=6334,66888$

Podría prescindir de tomar decimales pues sólo me interesa la parte entera, pero te dejo escrito todo por dos razones: la primera es para que puedas reconstruir los pasos que voy haciendo y la segunda es porque sería un error decir que $\log 2020^{2021}=6334$
Ahora tomo la parte entera del número que me ha salido antes: 6334; y le sumo 1. Consigo así el número 6335.

Con lo que ya hemos calculado cuántos dígitos son necesarios para escribir el número $2020^{2021}$ . Necesitamos 6335 dígitos (casi nada…).

Ya pero esto ¿para qué sirve?

Pues sirve para comparar números, aunque como te podrás imaginar no hay nadie que se dedique de forma profesional a contar cuántas cifras son necesarias para escribir un número, no obstante, de vez en cuando oirás habar de tal o cual número y sus dígitos, como por ejemplo en este artículo de la revista QUO donde dicen que hay un número con 23 millones de dígitos. De hecho, puedes calcular tú mismo cuántos dígitos tiene el número en cuestión:

[…] se consigue con el dos elevado a 77.232.917, menos uno. El número tiene nada menos que 23 millones de dígitos.
DESCUBREN EL NÚMERO PRIMO MÁS GRANDE DEL MUNDO (05-01-2018, Revista QUO. Consultado 22-09-2020)

El artículo anterior de la revista QUO no es baladí. Hay una lucha por ver quién puede conseguir calcular el número primo más grande, y puesto que son muyyyy grandes (y muy largos de escribir), no podemos compararlos por simple observación. Necesitamos otro método más sutil.

Debes tener en cuenta que un número es mayor que otro si tiene más dígitos, por lo que es una buena manera de comparar números relativamente grandes sin necesidad de calcularlos: «¿Tienes más dígitos? pues eres más grande».

Por ejemplo: ¿qué número es mayor $21^{2020}$ o $2020^{21}$ ?

Lo vamos a hacer calculando el número de dígitos de cada uno de ellos:

Número de dígitos de
- $\log 21^{2020}=2020\cdot \log 21=2670,88$
- Parte entera: 2670.
- Sumo uno: 2671.
- Por lo que el número de dígitos de $21^{2020}$ es de2671
Número de dígitos de :
- $\log 2020^{21}=21\cdot \log 2020= 69,41$
- Parte entera: 69.
- Sumo uno: 70.
- Por lo que el número de dígitos de $2020^{21}$ es de 70.

Así ya sabemos qué número es mayor sin necesidad de calcularlos:

$21^{2020}>2020^{21}$

Además $21^{2020}$ es mayor, con mucho, que $2020^{21}$ . ¡¡¡Es 2601 ordenes de magnitud mayor!! ¡¡ $10^{2601}$ !! ¡¡Un uno seguido de dos mil seiscientos un ceros!! Yo no sé tú, pero a mi este número se me escapa completamente de lo que puedo imaginar; solamente como referencia, se estima que el número de átomos del universo es $10^{80}$ . Sólo como referencia…

En este ejemplo era relativamente sencillo intuir qué número era mayor que otro simplemente fijándonos en las bases de las potencias y sabiendo algo sobre qué es una potencia y cómo se calcula; pero hay veces que estas cuestiones no se ven «a ojo».

Por ejemplo: ¿qué número es mayor $153^{50}$ o $202^{42}$ ?

En este caso no es nada fácil calcular qué número es mayor «a ojo» ya que la base menor está elevada a un mayor exponente, y no tenemos forma de saber a priori qué número es mayor. Por ello recurrimos a nuestro método basado en logaritmos:

Número de dígitos de
- $\log 153^{50}=50\cdot \log 153=109,23$
- Parte entera: 109.
- Sumo uno: 110.
- Por lo que el número de dígitos de $153^{50}$ es de 110.
Número de dígitos de
- $\log 202^{42}= 42\cdot \log 202=96,82$
- Parte entera: 96.
- Sumo uno: 97
- Por lo que el número de dígitos de $202^{42}$ es de 97.

Así, atendiendo al número de dígitos, ya sabemos qué número es mayor:

$153^{50}>202^{42}$

De hecho podemos decir que $153^{50}$ es trece, ¡¡TRECE!! órdenes de magnitud mayor: $10\ 000\, 000\, 000\, 000$ que se lee diez billones.

Y todo esto sin necesidad de calcular ninguna potencia. Por si te interesa, los números son:

$153^{50}=\phantom{\Huge H} 17162143 97056089 18740020 16570779 16796134 09088808 18077653 91896290 60536136 84319968 96099872 72619796 14522826 955249$
$202^{42}=\phantom{\Huge H}6679708597192190856336886681500530132237307932489770330890044457774962866463573155509919918587904$

Y te recuerdo que ambos números son mayores que el número de átomos estimados del universo.

Espero que con esta entrada te haya quedado claro qué es un logaritmo y cuál es su uso. Suele ser un concepto que cuesta algo al principio por la novedad, pero piensa que una vez tuviste que aprender a sumar y restar, luego a multiplicar y dividir… así que al final ya sabes que trabajando un poco podrás superarlo sin problemas.

Como siempre siéntete libre de dejar en comentarios cualquier opinión, duda o sugerencia.

Gracias por leerme

Si quieres contactar conmigo puedes hacerlo aquí

Si te gusta lo que hago y quieres invitarme a un café ¡¡te doy las gracias por adelantado!!

Vida de la entrada:

– 2020-10-05: Publicación.
– .2020-10-06: Corrección de erratas.

Bibliografía

Aparicio Peñas, A. M., Arribas Ruiz, F., González García, C., Llorente Medrano, J., Ruiz Jiménez, M.; 2015; Matemáticas aplicadas a las ciencias sociales (I); Ed. Editex; Madrid; ISBN: 978-84-9078-504-1.
Argüeso, M., Borobia, N., Lázaro, O., Pajares, A., Tomeo, V.; 2015; Matemáticas aplicadas a las ciencias sociales I; Ed. Paraninfo; Madrid; ISBN: 978-84-283-3548-5.
Colera Jiménez, J., Oliveira González, M. J., Gaztelu Albero, I., Colera Cañas, R.; 2016; Matemáticas orientadas a las enseñanzas académicas: 4 ESO; Ed. Anaya; Madrid; ISBN: 978-84-698-1069-9.
Linés Escardó, E.; 1991; Principios de análisis matemático; Ed. Reverté; Barcelona; ISBN: 978-84-291-5072-8.
http://blogs.hoy.es/curiosidades-cientificas/2019/12/27/cuantos-atomos-universo/ [22-09-2020].
https://www.quo.es/ciencia/a70038/numeros-primos/ [22-09-2020].