▶ 👍 Números irracionales 🥇
En esta entrada vamos a ver el último conjunto numérico con el que vamos a trabajar durante todo el año. Se trata de los números irracionales y complementan a los racionales para formar los números reales.
Los números irracionales
Los números irracionales son aquellos que poseen un desarrollo decimal, pero que no pueden expresarse mediante una fracción, esto es, no constituyen un número racional; su expresión decimal tiene un número infinito de cifras sin que se repita ningún patrón. Esto dicho así parece algo muy raro, pero seguro que lo vas a pillar rápido con los siguientes números que te pongo como ejemplos:
Ejemplos de números racionales:
Ejempos de números irracionales:
Pero ¿por qué surgen los números irracionales? La razón es que con los números racionales no podemos resolver ecuaciones como ![]() . Supongo que ya sabes que cuando en matemáticas se dice que no se puede resolver este tipo de ecuaciones en
. Supongo que ya sabes que cuando en matemáticas se dice que no se puede resolver este tipo de ecuaciones en ![]() , significa que no siempre se pueden resolver, como en el caso anterior; ya que, a veces, SI se pueden resolver, como en
, significa que no siempre se pueden resolver, como en el caso anterior; ya que, a veces, SI se pueden resolver, como en ![]()
Cuenta la historia que los números irracionales «nacieron» cuando un discípulo de la escuela pitagórica demostró la inconmensurabilidad de ![]() . La leyenda cuenta que Pitágoras mandó ahogar a su discípulo porque estos números invalidaban su paradigma filosófico.
. La leyenda cuenta que Pitágoras mandó ahogar a su discípulo porque estos números invalidaban su paradigma filosófico.
Necesidad de los números irracionales
A lo largo de toda la ESO has estado trabajando con números de los que no conocías el valor exacto. Esos cálculos son correctos ya que aproximaban de manera razonable al valor real, el cual no podías alcanzar ya que implicaba un número infinito de cálculos (aquellos que se realizan en la parte decimal). De lo que se trataba era de tener un algoritmo que nos permitiese calcular un número irracional con la aproximación (error) que deseemos.
Así, durante años has utlizado las siguientes aproximaciones de ![]() según necesitaras más o menos precisión, donde has aplicado los conceptos de aproximación y redondeo que ya conoces de otros cursos:
según necesitaras más o menos precisión, donde has aplicado los conceptos de aproximación y redondeo que ya conoces de otros cursos:
![]()
![]()
![]()
![]()
![]()
![]()
Ninguno de los números anteriores es exactamente ![]() , por eso no he usado un signo
, por eso no he usado un signo ![]() si no un signo
si no un signo ![]() . Lo que sí es verdad es que cada uno de los números anteriores se parece cada vez más al verdadero valor de
. Lo que sí es verdad es que cada uno de los números anteriores se parece cada vez más al verdadero valor de ![]() . De hecho, debajo de cada uno de los números anteriores tienes escrito cuál es el error cometido (símbolo
. De hecho, debajo de cada uno de los números anteriores tienes escrito cuál es el error cometido (símbolo ![]() ).
).
Los números reales
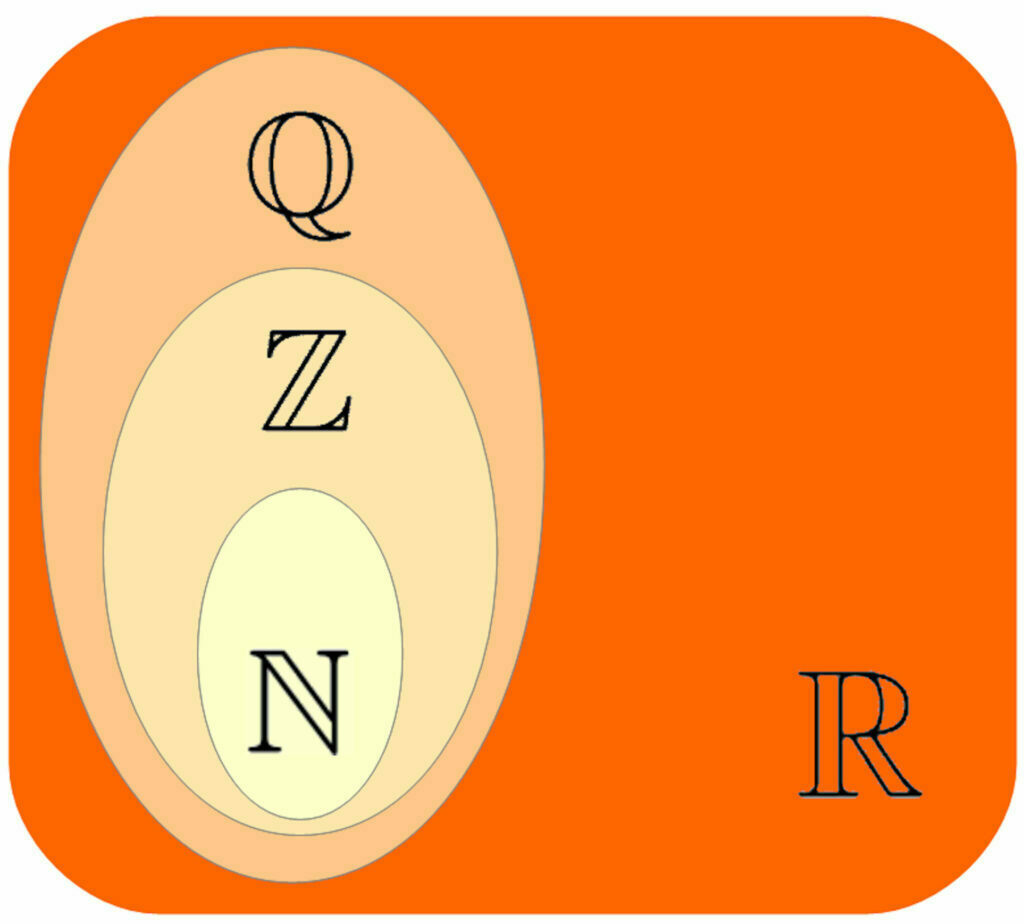
En la siguiente entrada hablaremos sobre los números reales, pero ahora tan sólo te quiero decir que éstos comprenden tanto a los números racionales como a los irracionales. Puedes decir que los números irracionales completan a los números racionales para, juntos, formar los reales.
En este esquema te intento representar lo que te acabo de decir. Como ves los números naturales forman un subconjunto de los enteros y éstos de los racionales; los racionales, a su vez, son un subconjunto de los reales (matemáticamente se escribe así ![]() )
)
Pero entonces ¿qué le falta a cada conjunto numérico para convertirse en el siguiente? Pues muy fácil:
- Si a los números naturales, les añadimos los números negativos, se convierten en los enteros.
- Si a los números enteros, les añadimos otros números que se pueden expresar como fracción, obtenemos los números racionales
- Si a los racionales les añadimos aquellos números que no se expresan como fracción (los irracionales), entonces obtenemos los números reales.
En este esquema, además, he querido señalarte otra cuestión, mucho más técnica, y que te voy a explicar muy brevemente, pero creo que debes saberlo para que puedas llegar a entender qué es eso del infinito (si es que hay alguien que realmente entiende el infinito). La cuestión es que hay muchísimos más números irracionales que racionales, por eso el hueco que he dejado para completar ![]() es mucho mayor que el propio conjunto
es mucho mayor que el propio conjunto ![]() .
.
Para mi fue una sorpresa cuando me dijeron que a pesar de que ![]() , resulta que existe la misma cantidad de cada uno de ellos (de forma matemática se dice que poseen el mismo cardinal, cosa que yo no te voy a explicar aquí). Ya te he dicho que esto es mucho, mucho más técnico. Pero el caso es que, si te pones a contar matemáticamente cuántos números hay en
, resulta que existe la misma cantidad de cada uno de ellos (de forma matemática se dice que poseen el mismo cardinal, cosa que yo no te voy a explicar aquí). Ya te he dicho que esto es mucho, mucho más técnico. Pero el caso es que, si te pones a contar matemáticamente cuántos números hay en ![]() ,
, ![]() ,
, ![]() , resulta que son mismos. Claro, que por «contar matemátcamente» no me refiero a ir diciendo uno, dos, tres…
, resulta que son mismos. Claro, que por «contar matemátcamente» no me refiero a ir diciendo uno, dos, tres…
Y entonces ¿también hay los mismos números reales que del resto? Pues no. Hay infinitos más. Y como puedes suponer, si la diferencia entre los reales y los racionales, son los irracionales, es que hay muchísimos más irracionales que racionales ¿no? Pues sí. La cantidad de números irracionales es infinitamente mayor que la de los racionales.
Como te he dicho, esta cuestión es muy técnica, y te lo quería contar como curiosidad. Así que si no lo entiendes demasiado o lo que aparece en este recuadro te parece complicado, puedes pasarlo por alto. Tu profe, que no te tiene manía, no te lo va a preguntar.
Representación de los números irracionales en la recta real
Lo primero que te tengo que decir es que no es fácil representar todos y cada uno de los números irracionales dentro de la recta real. Para el caso de los números racionales teníamos un algoritmo basado en el teorema de Thales. Pero en este caso no hay un algoritmo que nos permita calcular cualquier número irracional. A pesar de todo, podemos encontrar un algoritmo para representar raíces cuadradas ![]() y algunas razones trigonométricas.
y algunas razones trigonométricas.
Por mi experiencia, en clase de 4ESO y bachillerato sólo se representan raíces cuadradas. Es lo que te va a enseñar tu profesor, y es lo que debería contarte yo aquí para no entrar en camisas de once varas. A pesar de todo, aunque la entrada está dirigida a estudiantes de bachillerato y debería quedarme ahí; creo que es muy interesante introducir algo más de material extra que permita a los alumnos ir un poco más allá, si quieren. Por eso también voy a contar cómo representar algunas razones trigonométricas.
Representación de las raíces cuadradas
Para la representación de raíces cuadradas usamos el teorema de Pitágoras. La estrategia va a consistir en construir un triángulo rectángulo tal que uno de sus lados sea el número que queremos representar.
El ejemplo típico y con el que siempre se empieza es el de ![]() . Fíjate en la imagen siguiente. En ella puedes ver cómo se representa
. Fíjate en la imagen siguiente. En ella puedes ver cómo se representa ![]() en la recta real haciendo uso del teorema de Pitágoras. Voy a explicarte cómo puedes construir tú la misma figura:
en la recta real haciendo uso del teorema de Pitágoras. Voy a explicarte cómo puedes construir tú la misma figura:

 en la recta real.
en la recta real.- Lo primero que debes pensar es cómo conseguir el número
 . Si te das cuenta es la hipotenusa de un triángulo rectángulo de catetos de longitud
. Si te das cuenta es la hipotenusa de un triángulo rectángulo de catetos de longitud  .
. - Construyendo dicho triángulo (
 ), su hipotenusa tiene la longitud que necesitamos,
), su hipotenusa tiene la longitud que necesitamos,  .
. - Ahora con el compás trazas un arco hasta intersecar la recta real (el arco está marcado como
 y la interescción como
y la interescción como  ).
). - Si te fijas las coordenadas de
 son
son  . Evidentemente como no se puede escribir el número
. Evidentemente como no se puede escribir el número  completo, el ordenador ha elegido aproximarlo con un solo decimal.
completo, el ordenador ha elegido aproximarlo con un solo decimal.
Y ahora es tu turno: ¿cómo representarías los siguientes números: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ?
?
Representación de algunas razones trigonométricas
En 4ESO, dentro de las matemáticas académicas se estudia la trigonometría. Si ya te han introducido en el mundo de la trigonometría, conocerás la circunferencia goniométrica. Pues bien vamos a utilizar esa representación para hallar la representación en la recta real de las diferentes razones trigonométricas. Recuerda que:
 se mide en el eje
se mide en el eje  .
. se mide en el eje
se mide en el eje  .
. se mide sobre la recta
se mide sobre la recta 
- Además recuerda que no todas las razones trigonométricas son irracionales, por ejemplo
 que no es un número irracional.
que no es un número irracional.

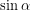 ,
,  y
y 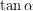 sobre la circunferencia goniométrica.
sobre la circunferencia goniométrica.Si te fijas un poco, ya tenemos todo lo que necesitamos. En este caso ¿qué es lo complicado? pues lo complicado es la medición del ángulo ![]() sin que nos equivoquemos, ya que puede no ser fácil dibujar un ángulo de digamos
sin que nos equivoquemos, ya que puede no ser fácil dibujar un ángulo de digamos ![]() . Pero una vez que hemos dibujado el ángulo, las razones trigonométricas aparecen inmediatamente por lo que lo único que debes es trasladarlas a tu recta real.
. Pero una vez que hemos dibujado el ángulo, las razones trigonométricas aparecen inmediatamente por lo que lo único que debes es trasladarlas a tu recta real.
Un último apunte sobre las funciones trigonométricas. Recuerda que, si trabajas en el cuerpo de los números reales las razones ![]() y
y ![]() SIEMPRE tienen un valor comprendido entre
SIEMPRE tienen un valor comprendido entre ![]() y
y ![]() siempre y cuando
siempre y cuando ![]() .
.
![]()
A continuación te dejo un vídeo que he grabado explicando cómo se representan números (racionales e irracionales) en la recta real.
Y ahora es tu turno: ¿conocías todas estas cuestiones de las que te he hablado? ¿te las han enseñado de otra manera? ¿se te hacen complicadas? Como siempre puedes dejar la respuesta a estas preguntas y cualquier otro comentario más abajo

Si quieres contactar conmigo puedes hacerlo aquí
Si te gusta lo que hago y quieres invitarme a un café 
Bibliografía:
- Aparicio Peñas, A. M., Arribas Ruiz, F., González García, C., Llorente Medrano, J., Ruiz Jiménez, M.; 2015; Matemáticas aplicadas a las ciencias sociales (I); Ed. Editex; Madrid; ISBN: 978-84-9078-504-1.
- Argüeso, M., Borobia, N., Lázaro, O., Pajares, A., Tomeo, V.; 2015; Matemáticas aplicadas a las ciencias sociales (I); Ed. Paraninfo; Madrid; ISBN: 978-84-283-3548-5.
- Colerus, E.; 1972; Breve historia de las matemáticas; 1ª edición; Doncel: libro joven de bolsillo; Madrid.
- Delgado Pineda, M.; Muñoz Bouzo, M. J.; 2010; Lenguaje matemático, conjuntos y números; Ed. Sanz y Torres; Madrid; ISBN: 978-84-82948-30-7.
- Lentin, A., Rivaud, J.; 1971; Álgebra moderna; 3ºed.; Ed. Aguilar; Madrid
Vida de la entrada:
– 2020-10-01: Publicación
–


