▶🎁 Números racionales (Bachillerato) 📖
[latexpage] Los números racionales ($\mathbb{Q}$) resuelven las ecuaciones que tienen la forma $ax+b=0$ y donde $a,b\in \mathbb{Z}$. En bachillerato se empieza por estudiar estos números ya que se suponen conocidos los números naturales ($\mathbb{N}$) y los números enteros ($\mathbb{Z}$). A pesar de ello, empezaremos hablando de la necesidad de los racionales.
Insuficiencia de los naturales (N) y los enteros (Z). Necesidad de los racionales (Q).
A continuación paso a explicarte muy brevemente por qué es necesario un nuevo conjunto numérico. Voy a decirte qué es lo que no se puede hacer tanto con los números naturales, $\mathbb{N}$, como con los números enteros, $\mathbb{Z}$.
Los números naturales, $\mathbb{N}$.
Los números naturales son aquellos que nos sirven para contar. ¿Contar el qué? Cualquier conjunto; sus elementos. Así es fácil ver que fueron los primeros números en aparecer ya que siempre se ha debido contar monedas, ganado, población…
Con los naturales se puede sumar y multiplicar, pero no siempre es posible restar o dividir. Con esta frase quiero decirte, que no siempre que restes o dividas dos números naturales, el resultado va a ser un número natural. Te lo explico con ejemplos:
- Sólo es posible restar números naturales si el sustraendo es mayor que el minuendo, por ejemplo:
$$7-5=2$$
Pero no es posible cuando el sustraendo es MENOR que el minuendo como en:
$$5-7=??$$
Como ves en la resta anterior el resultado no es un número natural, y por eso te lo marco con $??$ - Para dividir dos números naturales es necesario que el dividendo sea múltiplo del divisor, por ejemplo en:
$$48: 12=4$$
Pero no vas a poder dividir números naturales cuando el dividendo no es múltiplo del divisor, como en:
$$12:48=??$$
Al igual que antes con la resta, esta última división no tiene por resultado un número natural.
Las propiedades que tienen los números naturales respecto de la suma y la multiplicación son las siguientes:
Para la SUMA
- Propiedad asociativa:
$$a+(b+c)=(a+b)+c$$ - Elemento neutro:
$$a+0=0+a=a$$ - Propiedad conmutativa:
$$a+b=b+a$$
Para el PRODUCTO
- Propiedad asociativa:
$$a\cdot (b\cdot c)=(a\dot b)\cdot c$$ - Elemento neutro:
$$a\cdot 1=1\cdot a=a$$ - Propiedad conmutativa:
$$a\cdot b=b\cdot a$$
Para AMBAS: Propiedad distributiva
$$a\cdot (b+c)=a\cdot b+a\cdot c$$
Estas dos operaciones, con sus propiedades, confieren a los números naturales una estructura algebraica de la que no te voy a hablar aquí, pero que puedes consultar en la entrada si así lo deseas.
Lo importante es que tengas en mente que los números naturales no son suficientes para restar, y por tanto necesitamos ampliarlos para que esta operación siempre tenga sentido. Van a ser los números enteros, $\mathbb{Z}$.
Los números enteros, $\mathbb{Z}$.
Puesto que con los números naturales no se podía restar, los hemos ampliado y ahora podemos siempre resolver esta ecuación $a+x=0$. Ten en cuenta que lo único que nos está indicando esto es que SIEMPRE SE PUEDE RESTAR. Siguiendo con nuestros ejemplos anteriores, tenemos que:
$$7-5=2\qquad\qquad\qquad 5-7=-2$$
Como puedes ver, en ambos casos he podido restar ya que tanto $2$ como $-2$ son números enteros. Para decir que dos números pertenencen a un conjunto lo expresamos con el símbolo $\in$:
$$2, -2\in \mathbb{Z}$$
Entonces ¿qué problema hay con los enteros? pues que no siempre se puede dividir. Es el mismo problema que con los naturales, sólo puedo dividir, si el dividendo es múltiplo del divisor, y eso no siempre pasa.
Al igual que antes te he contado las propiedades que poseen los números naturales con la suma y la multiplicación, ahora te digo las propiedades de los enteros con la suma y el producto. Son las siguientes:
Para la SUMA
- Propiedad asociativa:
$$a+(b+c)=(a+b)+c$$ - Elemento neutro:
$$a+0=0+a=a$$ - Propiedad conmutativa:
$$a+b=b+a$$ - Elemento opuesto:
$$a+(-a)=(-a)+a=0$$
Para el PRODUCTO
- Propiedad asociativa:
$$a\cdot (b\cdot c)=(a\dot b)\cdot c$$ - Elemento neutro:
$$a\cdot 1=1\cdot a=a$$ - Propiedad conmutativa:
$$a\cdot b=b\cdot a$$
Para AMBAS: Propiedad distributiva
$$a\cdot (b+c)=a\cdot b+a\cdot c$$
Como ocurría con los números naturales, estas dos operaciones, con sus propiedades, confieren a los números enteros una estructura algebraica de la que tampoco te voy a hablar aquí, pero que puedes consultar en la entrada si así lo deseas.
Espero que te haya quedado claro que necesitamos un nuevo conjunto numérico donde siempre se pueda dividir, sin importar si el dividendo o el divisor son múltiplos o divisores el uno del otro. Este nuevo conjunto de números van a ser los números racionales.
¿Por qué necesitamos los números racionales?
Supongo que ya no tendrás dudas en comprender que la división no siempre se puede llevar a cabo en los números enteros (los números naturales pertenecen a los enteros; se dice que son un subconjunto de los enteros). Es posible que te sorprenda saber que las fracciones positivas se admitieron sin ningún impedimento mucho antes, incluso, que los números negativos; y es que si lo piensas un poco, es fácil comprender una fracción si la consideras como el reparto de una tarta entre varias personas, ¿pero qué es $-4$? ¿qué significa que yo tengo $-3\ euro$? ¿y que hay $-5º\ C$? Como puedes comprobar, la negatividad es un concepto más complicado que las fracciones.
El primer matemático del que se tiene constancia que estudió los números racionales (se representan con $\mathbb{Q}$) es Euclides en su libro VII de los elementos.
Aunque esta entrada trata de los números racionales, lo haré a nivel de bachillerato de ciencias sociales; por lo que si tu interés es ver una entrada más técnica sobre estos números, te recomiendo que le eches un vistazo a la construcción algebraica de los números racionales y sus propiedades.
¿Qué es una fracción?
Una fracción es una relación (cociente) entre dos números enteros $\displaystyle \frac{a}{b}$. El número de arriba ($a$) se llama numerador, mientras que el número de abajo ($b$) se llama denominador. ¿Cómo se interpreta una fracción? La forma en que yo la explico en los primeros curso de la ESO es la siguiente: el denominador indica el número de partes en que divides una cantidad (una tarta, dinero, tiempo…) y el numerador indica las partes con las que te quedas.
- Así $\displaystyle \frac{3}{8}$ indica que has dividido algo en $8$ partes y te quedas con $3$.
- Por otro lado $\displaystyle \frac{8}{3}$ indica que haces $3$ partes, pero te quedas con $8$.
Y esto último qué significa?, pues ni más ni menos que tomas más partes de que las en que has dividido la cantidad. Esto es, tan sólo, un número mayor que $1$. ¿Cuánto mayor que $1$? Pues las primeras $3$ partes forman la primera unidad, las segundas $3$ partes forman otra unidad (y ya van dos), y aún me quedan dos partes de las 8 que he decidido tomar, así que el número es $\displaystyle\frac{8}{3}=2+\frac{2}{3}$. Esta última expresión se denomina número mixto, pero no debes perder de vista que es un número racional. Lo único que has hecho ha sido tomar unidades enteras y luego sumarle un número racional que es menor que $1$.
Fracción equivalente
En el apartado anterior ya has visto que es posible escribir el mismo número de dos maneras distintas como: $\displaystyle \frac{8}{3}=2+\frac{2}{3}$. Pues bien, un número racional se puede escribir de muchas formas diferentes (de hecho, de infinitas maneras); por ejemplo, todas las fracciones siguientes representan el mismo número y se denominan fracciones equivalentes:
$$\frac{6}{8}=\frac{18}{24}=\frac{3}{4}=\frac{15}{20}=\frac{90}{120}=\frac{45}{60}=\cdots $$
y si todas estas fracciones representan el mismo número racional, ¿habrá alguna que sea la principal? Rotundamente SI. De todas las fracciones anteriores la principal es $\displaystyle \frac{3}{4}$ Se denomina representante canónico (en clase de secundaria se le llama fracción irreducible) y ahora te explico cómo calcularlo.
Supongo que ya sabrás calcular el mcd y mcm de dos números, y si aún no lo sabes, te recomiendo echar un vistazo a mi entrada sobre ello. Pues bien, si el mcd de numerador y denominador ES 1, entonces la fracción es irreducible y ése es el representante canónico; por el contrario, si el mcd es distinto de 1, lo que debes hacer es dividirlos por él; esto es, por ejemplo para $\displaystyle \frac{18}{24}$ como $mcd(18,24)=6$ puedes dividir tanto el $18$ como el $24$ por $6$ y así obtienes el representante canónico.
— Bueno, eso está bien, pero ¿no hay otra manera?, es que a mí me parece un rollo calcular el mcd.
Sí, hay otra manera, pero no es la forma académica y te va a llevar, probablemente más tiempo. Por ejemplo, puedes ir comprobando si tanto numerador como denominador son divisibles por el mismo número y así ir simplificando poco a poco la fracción, pero este método implica que tendrás que hacerlo varias veces. Aquí deberás usar los criterios de divisibilidad.
Vamos a volver a calcular la fracción irreducible de la fracción anterior, $\displaystyle \frac{18}{24}$:
$$\frac{18}{24}=\frac{9}{12}=\frac{3}{4}$$
Como ves, primero dividido por $2$ y luego por $3$.
También puedes descomponer uno de los dos (numerador o denominador) y ver si el otro se divide por alguno de ellos. Para seguir con nuestro ejemplo de $\displaystyle \frac{18}{24}$:
- $24=2^3\cdot 3$.
- $18$ se puede dividir por $6=2\cdot 3$, por lo que dividimos ambos por $6$.
Date cuenta que esta forma no es más ni menos que hallar el $mcd$ de ambos números de una forma un poco sui generis.
Con esto espero que te haya quedado claro qué es un representante canónico o fracción irreducible de un número racional. Y también espero que comprendas que es más fácil operar con los representantes canónicos que con una fracción no reducida. Supongo que esto te lo habrán dicho durante la ESO, y no te lo han dicho porque tu profe te tenga manía, si no porque es mucho más fácil operar así.
Te voy a mostrar (recordar, porque todo esto lo debes saber ya de la ESO) cómo se suman y como se multiplican números racionales (siempre en forma de fracción). ¿Y qué pasa con la resta y la división? La resta es sumar el opuesto, mientras que la división es multiplicar por el inverso, así que sabiendo cómo se suma y se multiplica, ya sabes cómo se resta y se divide.
Como se suman fracciones
Debes recordar que:
Sólo se pueden sumar fracciones que tienen igual denominador. Para ello, vas a necesitar calcular fracciones equivalentes.
Supongamos que queremos sumar las fracciones $\displaystyle \frac{5}{6}+\frac{7}{15}$ en este caso lo primero que debemos hacer es hallar el $mcm(6,15)=30$ y una vez hecho esto calcular las fracciones equivalentes de ambas. Así tenemos:
$$\frac{5}{6}+\frac{7}{15}=\frac{25}{30}+\frac{14}{30}=\frac{39}{30}=\frac{13}{10}$$
Como ves, una vez que tenemos el mismo denominador, lo único que hacemos essumar los numeradores de las fracciones equivalentes ($25+14=39$) y el último paso es SIEMPRE SIMPLIFICAR. Acostúmbrate a dar los resultados como una fracción irreducible.
Como se multiplican fracciones
La multiplicación de dos fracciones es mucho más sencilla.
Para multiplicar fracciones, multiplicamos los numeradores y los denominadores por separado.
Vamos a seguir operando con nuestras fracciones anteriores $\displaystyle \frac{5}{6}\cdot \frac{7}{15}$. La operación es tan sencilla como multiplicar $5\cdot 7=35$ y luego $6\cdot 15=90$
$$\frac{5}{6}\cdot \frac{7}{15}=\frac{35}{90}=\frac{7}{18}$$
Observa que al igual que antes, SIEMPRE SIMPLIFICO el resultado. Te vuelvo a insistir, tienes que dar los resultados como fracción irreducible.
Fracciones y números decimales
Hay otra forma de respresentar los números racionales que es mediante un número decimal. Estos números decimales pueden ser de varios tipos:
- Decimal exacto (DE): la cantidad de decimales es finita, como por ejemplo en $2,35; \ 4,78965; \ -3,12; \ -0,001$ Estos números pueden tener más o menos decimales, pero en algún momento se acaban. Y son números racionales como cualquier otro.
- Decimal periódico puro (DPP): en estos números la cantidad de decimales es infinita pero hay un patrón que se repite inmediatamente después de la coma, como por ejemplo: $3,234\ 234\ 234\ 234\ldots ; -3, 0012\ 0012\ 0012\ 0012\ldots$ El patrón que se repite se llama periodo y puede tener más o menos dígitos, pero siempre se repiten y en el mismo orden. También son números racionales.Te he marcado el período separando las cifras que se repiten, esta forma de representarlo no es del todo correcta y yo te lo he puesto así con fines didácticos. Es más correcto escribir un arquito o una linea sobre las cifras que se van repitiendo.
De esta manera, los números anteriores son: $3,\overline{234}$; $-3,\overline{0012}$. - Decimal periódico mixto (DPM): en este caso hay un patrón de dígitos que se repite indefinidamente pero entre la coma y ese patrón, existen unos cuantos números (que se llaman anteperiodo) que están en la parte decimal, pero no forman parte del periodo. Por ejemplo: $3,2\ 35\ 35\ldots$ $-3,500\ 49\ 49\ldots$ Por supuesto, también son números racionales. Al igual que antes te he marcado el período y el anteperíodo separando las cifras, pero no es del todo correcto. Lo correcto es escribir una raya sobre el período, dejando el anteperíodo fuera de este símbolo:.
Así, los números anteriores son: $3,2\overline{35}$; $-3,500\overline{49}$.
¿Existe una relación entre los números decimales (exacto, periódico puro o mixto) y las fracciones?
La respuesta fácil es SI. Pero lo interesante es que de un simple vistazo puedes saber si el número en cuestión será DP, DPP o DPM. Todo depende de la factorización del denominador de la fracción irreducible.
- Si el denominador, en su descomposición factorial, tiene sólo $2$ y $5$: por ejemplo $5=5$, $2=2$; $10=2\cdot 5$; $8=2^3$; $150=2^3\cdot 5^2\ldots$ Todos estos denominadores dan como resultado números decimales exactos.
- Si el denominador, en su descomposición factorial, no tiene ni $2$ ni $5$: por ejemplo $3=3$; $21=3\cdot 7$; $13=13$; $39=3\cdot 13\ldots$ Todos estos denominadores dan por resultado un número decimal periódico puro.
- Si en denominador, en su descomposición algún $2$, algún $5$ y algún otro número: por ejemplo $6=2\cdot 3$; $15=3\cdot 5$; $24=2^3\cdot 3\ldots$ Todos estos denominadores dan por resultado un número decimal periódico mixto (piensa que estos números son una mezcla de $2$, $5$ y algo más; y mixto no deja de significar mezcla).
En definitiva, debes seguir este esquema que te pongo a continuación:

Ahora la pregunta del millón es: ¿Cómo podemos pasar de fracción a número decimal y de número decimal a fracción? es evidente que si un número racional se puede representar como una fracción o un número decimal, tendrá que haber alguna manera de pasar de una forma a la otra…
- Para pasar de fracción a número decimal, lo que debes hacer es, tan sólo, dividir.
- Para pasar de número decimal a fracción, hay que calcular la fracción generatriz, que es lo que te explico en los siguientes puntos.
Cálculo de la fracción generatriz
Cuando tienes un número racional expresado en forma de número decimal, muchas veces es más útil emplear su forma de fracción para operar en vez de hacerlo mediante decimales, de hecho casi siempre es mejor operar con fracciones en vez de con números decimales; y esto es especialmente útil si el número decimal es no exacto, es decir es un número periódico puro y periódico mixto.
Yo te voy a explicar el método tal y como es. Sé que hay reglillas («pon tantos $9$ como cifras del período y …»), pero eso no es hacer matemáticas, eso es una receta. Lo que vamos a hacer es plantear una serie de ecuaciones que nos permitan llegar a una fracción, y probablemente no sea una fracción irreducible, por lo que siempre habrá que simplificar. El objetivo siempre va a ser eliminar la parte decimal del número.
Fracción generatriz de un número decimal exacto
Sin duda este es el apartado más fácil de todos.
La receta dice que lo que debes hacer es escribir una fracción donde en el numerador pongas el número decimal SIN parte decimal (es decir, te olvidas de la coma) y en el denominador un $1$ seguido de tantos ceros como dígitos tenga la parte decimal.
Por ejemplo, para el número $4, 375$ debes proceder de la siguiente manera:
$$4,375=\frac{4375}{1000}=\frac{35}{8}$$
Ahora vamos a ver como llegar hasta aquí RAZONANDO.
- A nuestro número lo vamos a llamar $N$. Lo podría haber llamado con otra letra, pero puesto que la palabra número empieza por N, así está bien.
$$N=4,375$$ - Ahora pienso ¿por cuánto tengo que multiplicar a $N$ para eliminar la parte decimal? cuando digo eliminar significa que no forme parte de la parte decimal, si no de la parte entera. Multiplicando $N$ por $1000$ cumplo lo anterior, luego tengo que:
$$1000N=4375$$ - Y esto es una ecuación donde la incógnita es $N$ en lugar de $x$, así que simplemente resuelvo
$$N=\frac{4375}{1000}$$ - ¿Adivinas cuál es el último paso? Efectivamente, simplificar la fracción:
$$N=\frac{35}{8}$$
Creo que con este ejemplo es suficiente, así que ahora no tendrás problema en calcular por tí mismo las siguientres fracciones generatrices de los siguientes números decimales exactos:
- $3,1415$ Esto NO es $\pi$
- $-8,42$
- $-10,01$
Fracción generatriz de un número decimal periódico puro
Cuando nos enfrentamos a un número racional en forma de decimal periódico puro, debemos saber cuántos dígitos componen el período, pero esto es muy fácil: sólo tienes que contarlos.
Ejemplo 1
Imagina que nos dan el nímero $N=4,\overline{375}=4,375375375\ldots$ y tenemos que hallar su fracción generatriz. La idea es que busquemos la forma de mover el período, de tal manera que luego podamos restar y quedarnos sólo con un número entero. Esto parece un trabalenguas, pero ya verás como no es tan difícil como parece. Sigamos.
Puesto que este número tiene 3 dígitos en el período, podemos multiplicarlo por 1000 y obtenemos lo siguiente $1000N=4375,3753753\ldots$ Y tú puedes decir «pues tampoco hemos avanzado mucho», bueno, ahora podemos colocarlos de la siguiente manera:
\begin{equation*}
\begin{aligned}
1000N=&4375,375375375\ldots\\
1N=&\phantom{437}4,375375375\ldots
\end{aligned}
\end{equation*}
Y si ahora restas ambos números ¿qué le ocurre a la parte decimal? Desaparece. Pero es muy importante que hayas multiplicado el número $N$ por $1000$ si lo multiplicas por otro número no se quedan las partes decimales colocadas. Así, una vez que hemos restado, obtenemos:
$$999N=4371$$
Y esto es muy, pero que muy fácil de resolver. El número racional que estamos buscando es (ya te doy la fracción simplificada y todo):
$$N=\frac{4371}{999}=\frac{1457}{333}$$
Te voy a hacer otro ejemplo.
Ejemplo 2
Supongamos que quiero hallar la fracción generatriz del número $N=2,010101010\ldots$ Lo primero en que me fijo es que el período tiene dos dígitos que se repiten: $01$, por tanto, si antes multiplicaba el número por $1000$ porque el período tenía tres dígitos, ahora que tiene dos dígitos ¿por cuánto he de multiplicar? Exacto por $100$. Así ya puedo preparar la resta:
\begin{equation*}
\begin{aligned}
100N=&201,01010101\ldots\\
1N=&\phantom{20}1,01010101\ldots
\end{aligned}
\end{equation*}
Y si ahora restamos, obtenemos una ecuación en $N$ muy fácil de resolver:
$$99N=200\quad\Longrightarrow\quad N=\frac{200}{99}$$
Y resulta que esta fracción es irreducible, así que esta es la solución.
Fracción generatriz de un número decimal periódico mixto
Ahora vamos a subir un nivel y vamos a complicarlo todo un pelín más. ¿Qué le sobra a un número DPM para convertirse en DPP? Efectivamente, el anteperiodo. Si no tuviera anterperiodo se trataría de un número periódico puro.
Pues el primer paso que vamos a hacer es multiplicar el número que nos dan para convertirlo en un número DPP. Vamos a verlo con tres ejemplos:
Ejemplo 1
Vamos a calcular la fracción generatriz del número $N=4,375757575\ldots=4,3\overline{75}$. Se trata de un número DPM y su anteperíodo es de un único dígito, luego si multiplico por $10$, obtengo $10N=43,\overline{75}$ que ya es un número DPP. Y ahora sólo debo aplicar el caso del apartado anterior, pero teniendo en cuenta que no parto de $N$ si no de $10N$:
\begin{equation*}
\begin{aligned}
1000N=&4375,757575\ldots\\
10N=&\phantom{43}43,757575\ldots
\end{aligned}
\end{equation*}
¡¡Atención!! El número DPP al que estoy calculando su fracción generatriz es $10N=43,\overline{75}$. Ten cuidado porque no es raro ver que alguien se confunde en este paso.
El caso es que si resto los números anteriores obtengo lo siguiente:
$$990N=4332\quad \Longrightarrow\quad N=\frac{4332}{990}=\frac{722}{165}$$
Voy a hacerte otro ejemplo para poder verlo todo más claro.
Ejemplo 2
En este caso, vamos a calcular la fracción generatriz del DPM $N=12,22\overline{13}$. Lo primero que vemos es que el anteperiodo tiene dos dígitos, por lo que para «convertir» al número en un DPP tenemos que multiplicar por $100$: $100N=1222,\overline{13}$. Y ahora que sabemos que estamos tratando con un DPP, tan sólo debemos hallar su fracción generatriz:
\begin{equation*}
\begin{aligned}
10000N=&122213,131313\ldots\\
100N=&\phantom{12}1222,131313\ldots
\end{aligned}
\end{equation*}
Si ahora resto y opero los anteriores números obtengo:
$$9900N=120991\quad\Longrightarrow\quad N=\frac{120991}{9900}$$
Que resulta ser un fracción irreducible.
Ejemplo 3
Vamos a calcular la fracción generatriz del siguiente número DPM $N=98,956\overline{42}$ Para empezar vemos que este número tiene un anterperiodo de tres dígitos, así que lo primero es «convertirlo» en un DPP multiplicándolo por $1000$. Así obtenemos $1000N=98956,\overline{42}$ y ahora que tenemos un DPP sólo tenemos que calcular su fracción generatriz:
\begin{equation*}
\begin{aligned}
100000N=&9895642,42424242\ldots\\
1000N=&\phantom{98}98956,42424242\ldots
\end{aligned}
\end{equation*}
Y operamos:
$$99000N=9796686\quad \Longrightarrow\quad N=\frac{9796686}{99000}=\frac{1632781}{1650}$$
Representación en la recta de los racionales
Seguro que tu profe, que no te tiene manía, te habrá mostrado muchas veces una recta donde ha ido localizando los distintos números. Esa recta se va a acabar llamando recta real y en este apartado te voy a mostrar cómo localizar los números racionales en la recta real. Para ello debemos echar mano del teorema de Thales, así que te recomiendo que le des un vistazo para recordar de qué trata.
Vamos a localizar los siguientes números: $\displaystyle \frac{2}{3},\ \frac{4}{5},\ \frac{10}{9},\ \frac{12}{7},\ \frac{34}{15}$
En primer lugar, para aquellos números anteriores que son mayores que $1$, vamos a transformarlos en números mixtos. Yo te los voy a volver a poner todos y aquellos que pueda los transformaré a números mixtos:
- $$\displaystyle \frac{2}{3}= \frac{2}{3}$$
- $$\displaystyle \frac{4}{5}= \frac{4}{5}$$
- $$\displaystyle \frac{10}{9}= 1+\frac{1}{10}$$
- $$\displaystyle \frac{12}{7}= 1+\frac{5}{7}$$
- $$\displaystyle \frac{34}{15}=2+\frac{4}{15}$$
Ejemplo 1: representación de $\displaysytle \frac{2}{3}$
Voy a empezar por ponerte la solución en una imagen y posteriormente te lo voy a ir explicando (el número racional $2/3$ está representado por el punto $K$, en rojo):
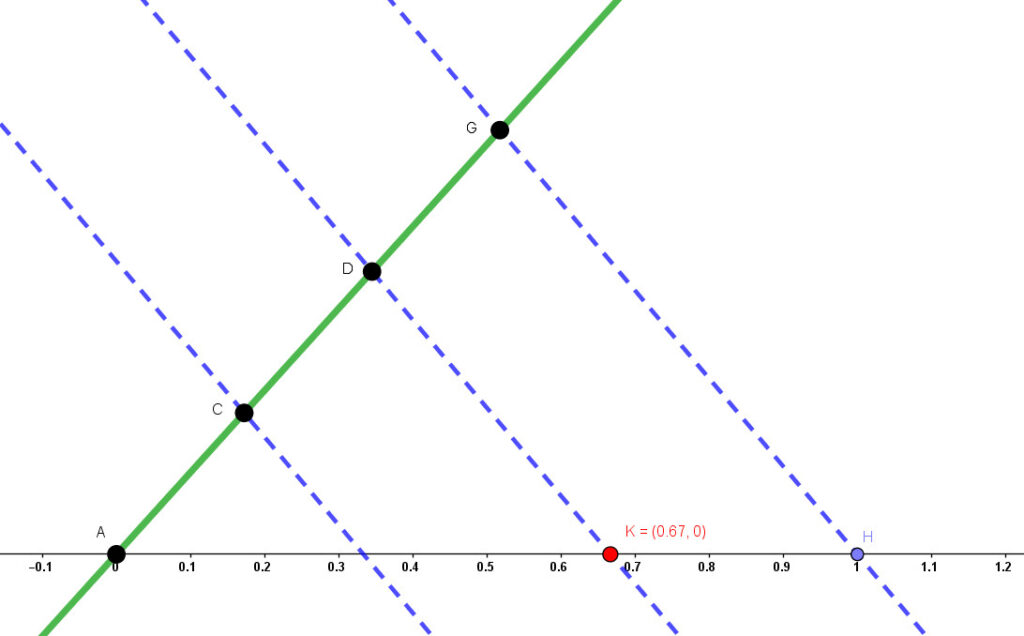
Lo primero es identificar cada una de los elementos que aparecen en el dibujo:
- La línea recta horizontal (en negro) va a ser nuestra recta real y en ella es donde tenemos que ir localizando todos los números racionales.
- La línea verde, oblicula, es una recta auxiliar y luego te diré para qué la vamos a usar.
- Las líneas azules, discontinuas, son también auxiliares y nos van a ayudar a localizar el número racional.
- Los puntos $A,C,D,G$ también son auxiliares y lo importnante es que equidistan, esto es: $\overline{AC}=\overline{CD}=\overline{DG}$
- El punto $A$ es el lugar donde se ubica nuestro $0$ y también donde se intersecan la recta real con la recta auxiliar.
- El punto $H$, en azul, indica la unidad; es decir, es donde hemos localizado el número $1$.
Seguro que este dibujo te recuerda al teorema de Thales. ¡¡Eso es porque vamos a usar el teorema de Thales para localizar cualquier número racional!!
Te explico cómo ir dibujando todo lo que aparece, pero si has manejado el teorema de Thales, todo lo que te voy a contar ya lo sabes:
- En primer lugar trazamos una línea auxilar (la verde). Da igual con qué ángulo la traces.
- En segundo lugar marcamos los puntos $A,C,D,G$ sobre esa línea auxiliar. Es muy importante que sean EQUIDISTANTES. El punto $A$ es la intersección de la recta auxiliar y la horizontal; luego, en el fondo, sólo hemos marcado tres puntos: $C,D,G$. Fíjate que hemos marcado tres puntos y el denominador es un $3$.
- Lo tercero es trazar la recta que pasa por $G$ y por $1$.
- En cuarto lugar es trazar paralelas a la recta anterior que pasen por los puntos $C$ y $D$.
- Lo último que tenemos que hacer es localizar el número $2/3$. Y esto es tan fácil como contar las intersecciones de las rectas azules con la recta horizontal y elegir la segunda empezando a contar desde el $0$ o el punto $A$, que son lo mismo.
Y así hemos localizado el número $2/3$. Todos los números racionales se localizan de esta manera (ahora te voy a hacer otros ejemplos); distinto es para los irracionales, pero eso es otra entrada.
Ejemplo 2: representación de $\displaysytle \frac{4}{5}$
La explicación, y el dibujo, de cómo representar el número racional $4/5$ es exactamente igual que para el $2/3$.
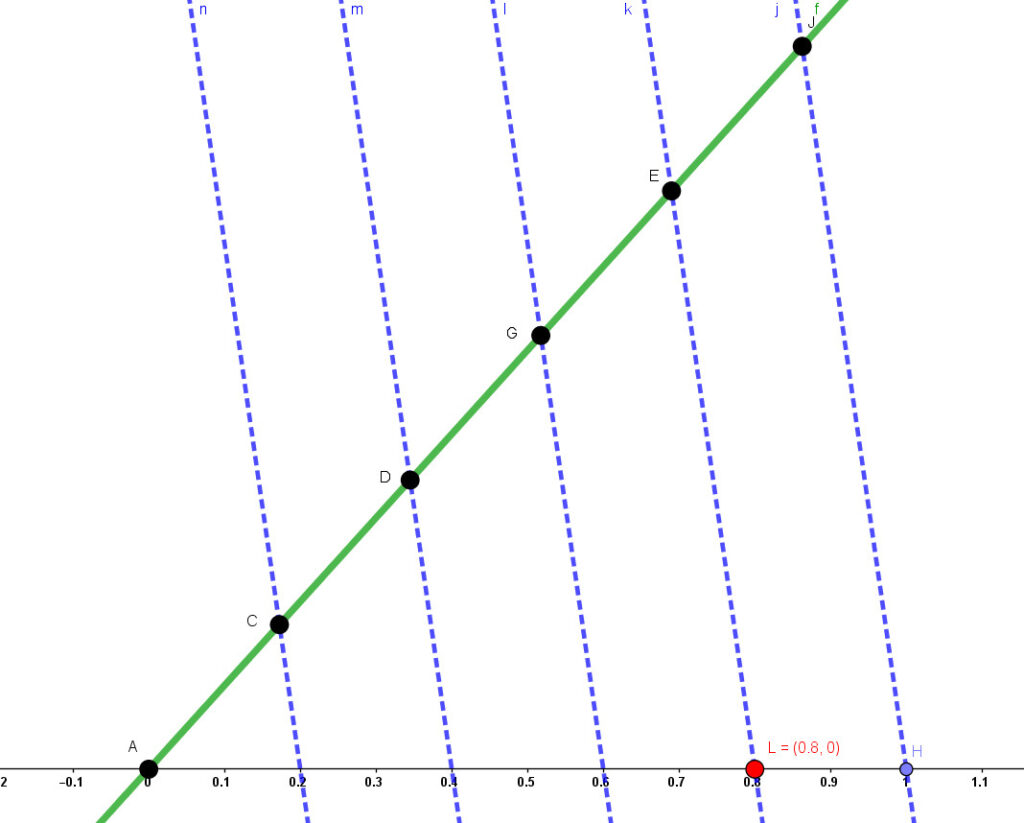
- Igual que en el caso anterior, en primer lugar trazamos una línea auxilar (la verde).
- En este ejemplo, como el número racional a representar es $4/5$ debemos marcar los puntos $A,C,D,G, E, J$ sobre esa línea auxiliar. Es muy importante que sean EQUIDISTANTES. El punto $A$ es la intersección de la recta auxiliar y la horizontal; luego, en el fondo, sólo hemos marcado cinco puntos: $C,D,G,E,J$. Fíjate que hemos marcado cinco puntos y el denominador es un $5$.
- Lo tercero es trazar la recta que pasa por $J$ y por $H$. El punto $H$ es donde hemos localizado nuestra unidad (nuestro $1$).
- En cuarto lugar debes trazar paralelas a la recta anterior que pasen por los puntos $C$, $D$, $G$ y $E$.
- Lo último que tenemos que hacer es localizar el número $4/5$. Y esto es tan fácil como contar las intersecciones de las rectas azules con la recta horizontal y elegir la cuarta empezando a contar desde el $0$ o el punto $A$, que son lo mismo.
- Así hemos localizado el punto $L$, cuya abscisa es precisamente $4/5$.
Ejemplo 3: representación de $\displaysytle 1+\frac{1}{10}$

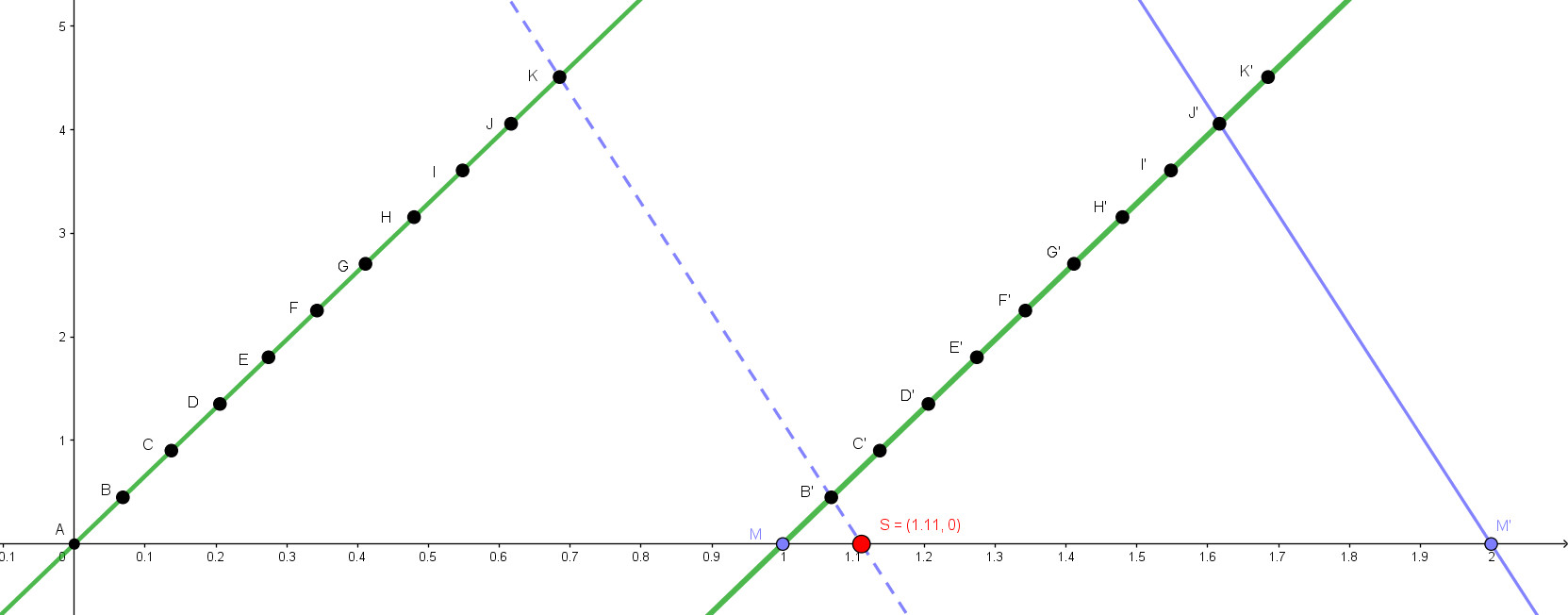
Representación del número racional 10/9 aplicando el teorema de Thales. Se calcula cuánto es 1/9 y se toman 10 partes 
Representación alternativa del número racional 10/9 utilizando el teorema de Thales.
Antes de nada debes darte cuenta que la escala de los ejes no es la misma en el de abscisas y en el de ordenadas. Una vez que tengas esto en cuenta, podemos comenzar la representación del número.
En estos casos, cuando los números racionales son mayores que $1$ se puede actuar de dos formas distintas:
- Imagen de la izquierda. De la misma forma que hemos venido haciéndolo hasta ahora: en nuestro caso implica localizar $9/9$, que es el punto $J$ y unir dicho punto con el $1$; y luego añadir $1/9$ más.
- Imagen de la derecha. A partir del número mixto: en nuestro caso como es $\displaystyle \frac{10}{9}=1+\frac{1}{9}$ tendremos que añadir $1/9$ al número $1$
Te lo explico un poco más pormenorizadamente.
Imagen de la izquierda
Vamos a partir de lo que sabemos y veremos qué ocurre cuando el número racional es mayor que $1$.
- Como se trata de una fracción cuyo denominador es un $9$, en la recta auxiliar dibujamos $9$ puntos equidistantes, y trazamos la recta $JM$.
- Si tuviéramos que representar un número menor que $1$, como $4/9$ lo que hay que hacer es trazar paralelas hacia la izquierda de la recta $JM$ y así podemos hallar $1/9,\ 2/9,\ 3/9=1/3,\4/9,\ 5/9,\ 6/9=2/3,\ 7/9,\ 8/9,\ 9/9=1$
- Como el número $10/9$ es mayor que $1$ tendremos que trazar una paralela hacia la derecha de la recta $JM$, la pregunta es ¿por dónde?
- Tendremos que buscar un punto $K$ tal que sea $\overline{KJ} =\overline{JI} =\overline{IH} =\overline{HG} =\overline{GF} =\overline{FE} =\overline{ED} =\overline{DC} =\overline{CB} =\overline{BA}$
- ¿Y cómo conseguimos ese punto $K$? Fácil, cuando hagamos las marcas en la recta verde, en vez de localizar 9 marcas, ponemos 10, que son las que vamos a necesitar.
Date cuenta que así hemos hallado un punto $S$ que representa el número racional $10/9$
Imagen de la derecha
En este caso, partimos del número mixto $\displaystyle 1+ \frac{1}{9}$ y ¿cómo podemos interpretar esto? pues muy fácil, significa «añade $1/9$ al número $1$. Así pues, si ya estamos en el número $1$ tan sólo debemos encontrar cuánto es $1/9$ y «colocarlo» a la derecha. ¿Y cómo calculamos ese $1/9$ extra? exactamente igual que en los primeros casos.
He querido dejarte escritos los elementos que hemos utilizado en la imagen de la izquierda para que veas que en el fondo, estamos haciendo lo mismo. Lo único que tienes que tener en cuenta es que en vez de llamar a los puntos $B,C,D,E,F,G,H,I,J,K,M$, los he denominado $B’,C’,D’,E’,F’,G’,H’,I’,J’,K’,M’$ Pero es importante que entiendas y comprendas que estamos haciendo lo mismo en ambas figuras.
Como los dos siguientes ejemplos que te voy a ofrecer, son de números mayores que $1$, cada uno de ellos lo haré de una manera diferente de las dos que te he mostrado aquí.
Ejemplo 4: representación de $\displaystyle \frac{12}{7}= 1+ \frac{5}{7}$

Como en el caso anterior para representar este número racional, procedemos de la siguiente manera:
- Trazamos una recta auxiliar (verde), sobre la que realizamos tantas marcas como nos indica el denominador: 7. Estas marcas son equidistantes
- Localizamos la séptima marca ($H$) y lo unimos con nuestra unidad (punto $A’$). Dibujamos la recta $HA’$ (azul).
- Como el numerador (12) es mayor que el denominador, sobre la recta verde realizamos 5 marcas más, y llegamos así a la marca $M$.
- Trazamos una paralela a la recta $HA’$ que pasa por $M$ y corta a la recta real en el punto $Q$, que es la solución buscada.
Ejemplo 5: representación de $\displaysytle \frac{34}{15}= 2+ \frac{4}{15}$

En este caso partimos del número mixto, es decir que debemos añadir $\displaystyle \frac{4}{15}$ a la derecha del $2$. Para ello:
- Dibujamos una recta auxiliar que pasa por la marca de $2$, aquí está representado por el punto $A»$.
- Sobre esa recta hacemos tantas marcas, equidistantes, como nos indique el denominador, es decir $15$ y llegamos hasta la $P»$.
- Trazamos la recta que pasa por $P»$ y por el número $3$, que está representado por el punto $A»$. Es decir, trazamos la recta $A»P»$
- Trazamos una paralela a la recta anterior que pase por la cuarta marca, $E»$, (recta azul discontinua) y que corta a la recta real en el punto $Q$.
- El punto $Q$ es la solución.
Con esto dejamos el tema sobre los racionales. Espero que te haya servido de ayuda. La siguiente entrada será sobre los irracionales ($\mathbb{I}$) que son los números que… bueno, eso mejor te lo cuento en la próxima entrada.
A continuación te dejo un vídeo que he grabado explicando cómo se representan números (racionales e irracionales) en la recta real.
Como de costumbre si quieres comentar algo, necesitas una aclaración o quieres que trate un tema en concreto, no dudes en escribirlo en los comentarios

Si quieres contactar conmigo puedes hacerlo aquí
Si te ha gustado lo que has leído y quieres invitarme a un café ☕, te doy las gracias por adelantado.
Bibliografía:
- Aparicio Peñas, A. M., Arribas Ruiz, F., González García, C., Llorente Medrano, J., Ruiz Jiménez, M.; 2015; Matemáticas aplicadas a las ciencias sociales (I); Ed. Editex; Madrid; ISBN: 978-84-9078-504-1.
- Argüeso, M., Borobia, N., Lázaro, O., Pajares, A., Tomeo, V.; 2015; Matemáticas aplicadas a las ciencias sociales (I); Ed. Paraninfo; Madrid; ISBN: 978-84-283-3548-5.
- Delgado Pineda, M.; Muñoz Bouzo, M. J.; 2010; Lenguaje matemático, conjuntos y números; Ed. Sanz y Torres; Madrid; ISBN: 978-84-82948-30-7.
Vida de la entrada:
– 2020-09-28: Publicación.
– 2020-09-30: Añadida infografía.