📚 ▶ Operar con polinomios 🥇
Hola profemaniático, pues resulta que aquí estás porque tienes que aprender polinomios. ¡¡Menuda faena!! pero déjame decirte antes una cosa: no es tan fiero el león como lo pintan, así que si dedicas un rato a lo que te voy a contar, vas a acabar siendo el mejor en polinomios de tu instituto.
Antes de nada me gustaría decirte que tengo otras dos entradas que quizá te interesen: una dedicada a los monomios, en la que te explico qué son y cómo se operan; y otra dedicada a la factorización de los polinomios. En esta entrada me dedicaré a contarte como sumar, restar, multiplicar y dividir polinomios.
Las tres primeras operaciones aritméticas con polinomios son sencillas: la suma, la resta y la multiplicación de polinomios no es más que una generalización de las propias que se hacen con monomios. La división tiene algo más de enjundia, sobre todo porque requiere gran cantidad de concentración para no equivocarte. No obstante, existe una forma sencilla de proceder a la división de polinomios que es la regla de Ruffini, que te cuento en otra entrada.
Así que lo que tienes que tener presente es lo que te propongo en este esquema.

Como ya habrás tenido oportunidad de comprobar, los polinomios pertenecen a la rama del álgebra y la primera vez que te encontraste con ellos fue en 1ESO, donde te explicaron los monomios; en 2ESO ya aparecieron los polinomios y llegarías hasta a dividir un polinomio por un monomio; y es en 3ESO cuando aparecen en todo su esplendor y ya tienes que dividir polinomios entre polinomios y factorizarlos. A partir de entonces os podéis considerar como viejos amigos.
Qué es un polinomio
Si has leído la entrada sobre monomios, habrás visto que ahí te lo explico todo con pelos y señales, así que ahora sólo te voy a recordar las cuestiones más importantes:
- Un polinomio se nombra con una letra mayúscua (se suelen usar
 ) y entre paréntesis la variable(s) de las que consta. Por ejemplo,
) y entre paréntesis la variable(s) de las que consta. Por ejemplo,  es un polinomio, cuya variable es
es un polinomio, cuya variable es  ; mientras qeu
; mientras qeu  es un polinomio cuyas variables son
es un polinomio cuyas variables son  e
e  ; por otro lado
; por otro lado  es un polinomio en el que te encontrarás tres variables:
es un polinomio en el que te encontrarás tres variables:  .
. - Un polinomio es la unión de varios monomios mediante sumas o restas. Por ejemplo
 es un polinomio formado de 4 monomios.
es un polinomio formado de 4 monomios. - El grado de un polinomio es el grado de su monomio de mayor grado. En el caso del anterior polinomio
 su grado es
su grado es  porque el monomio de mayor grado es
porque el monomio de mayor grado es  que posee grado 5.
que posee grado 5. - El coeficiente del monomio de mayor grado se llama coeficiente director o coeficiente principal. En nuestro caso, el coeficiente director de
 es 3.
es 3. - El monomio de grado cero (es un número que no va acompañado de incógnita) se denomina término independiente. En nuestro anterior ejemplo, el término independiente es 9.
- Puede ocurrir que un polinomio no tenga término independiente como
 en este caso el término independiente es 0.
en este caso el término independiente es 0.
Como has visto, en la lista anterior te he dado un pequeño resumen sobre qué debes saber como mínimo de polinomios. Ahora vamos a empezar a ver cómo se operan. En concreto vamos a ver la suma, la resta, el producto por escalares, el producto entre polinomios y la división de un polinomio por otro polinomio. Ya te he dicho que la factorización y la regla de Ruffini, se quedan para otra ocasión.
Cuéntame más de la aritmética de polinomios
Voy a dividir esta sección en varias partes: suma, resta, multiplicación por escalar, multiplicación de polinomios y división de polinomios. Como puedes comprender no te voy a hablar de la división por un escalar, ya que dividir por un número es multiplicar por su inverso.
Te recomiendo que tomes papel y lápiz para ir haciendo poco a poco lo que yo te voy a ir contando. 

Consejos básicos para operar
A continuación te dejo una serie de consejos que yo doy a mis alumnos para que puedan operar polinomios con éxito, y sobre todo sin posibilidad de equivocación:
- En la ESO y bachillerto, los polinomios con los que vas a tener que enfrentarte son aquellos escritos en una única variable, normalmente será
 ; eso implica que la parte literal de cada uno de los monomios con los que operes va a ser de la forma
; eso implica que la parte literal de cada uno de los monomios con los que operes va a ser de la forma  siendo
siendo  Dicho de otra manera, no te vas a encontrar cosas como
Dicho de otra manera, no te vas a encontrar cosas como  o como
o como  (por cierto, esta última es la ecuación de una circunferencia).
(por cierto, esta última es la ecuación de una circunferencia). - Los monomios los debes operar según su grado. Como todos los monomios con los que vas a operar tienen su parte literal que será una potencia de
 , debes operar según su grado. En particular, debes tener en cuenta que
, debes operar según su grado. En particular, debes tener en cuenta que  o
o  no dejan de ser unas potencias, y si las debes sumar debes seguir las normas establecidas para ello. Así que no puedes decir que
no dejan de ser unas potencias, y si las debes sumar debes seguir las normas establecidas para ello. Así que no puedes decir que 
o cosas peores que he llegado a ver
. Si haces tal cosa, y en función de en qué curso estés; tu profe, que no te tiene manía, va a penalizarte o a anularte toda la pregunta del examen.
- En los resultados finales, sólo debe aparecer, como mucho, un único monomio de cada grado, y preferiblemente ordenados. Es decir, si tu resultado es
 lo correcto es que escribas:
lo correcto es que escribas: 
- Siempre debes tener presente que aparecerán espías
Ya sabes, aquellos coeficientes, exponentes o monomios enteros que están escondidos: no los ves pero debes tenerlos en cuenta. Puedes estar seguro de que aparecerán varias veces a lo largo de un solo ejercicio.
Suma de polinomios
Para sumar polinomios lo que hacemos es ir sumando poco a poco los monomios de igual grado.

Por ejemplo, si tenemos ![]() y
y ![]() Podemos sumarlos de la siguiente manera:
Podemos sumarlos de la siguiente manera:
![]()
No obstante, creo que realizar la suma en linea puede ser, a veces, confuso y por eso recomiendo que lo pongas de la siguiente manera:
![Rendered by QuickLaTeX.com \[\begin{aligned} A(x)=&5x^6 \phantom{+..x^5} -2x^3 +3x^2 \phantom{-x+} -2\\ B(x)=& \phantom{5x^6+.}x^5 -5x^3+3x^2 -x+10\\\hline A(x)+B(x)=& 5x^6+x^5 -7x^3+6x^2-x+8\end{aligned}\]](https://www.cursomates.com/wp-content/ql-cache/quicklatex.com-f4fd03fe9a5ba0ba8e3e92d1456c2f60_l3.png)
Creo que de esta manera se ve mucho mejor todo y, sobre todo, al colocar cada monomio en su columna (como ves hay una columna preparada para cada monomio en función de su grado) lo que obtienes es que no te dejas nada sin operar.
Resta de polinomios
La resta de polinomios se hace igual que la suma, pero con una salvedad. El sustraendo cambia el signo de todos y cada uno de sus monomios.

Si operamos con los polinomios anteriores: ![]() y
y ![]() ; y ahora lo que queremos es restar
; y ahora lo que queremos es restar ![]() debes tener en cuenta que mientras que
debes tener en cuenta que mientras que ![]() resulta que
resulta que ![]() y ahora sí, podemos sumar
y ahora sí, podemos sumar ![]()
Voy a restarlos pero ya te los escribo en forma de la tabla que te escribí en el apartado anterior:
![Rendered by QuickLaTeX.com \[\begin{aligned} A(x)=&5x^6 \phantom{+..x^5} -2x^3 +3x^2 \phantom{-x+} -2\\ -B(x)=& \phantom{5x^6}-x^5 +5x^3-3x^2 +x-10\\ \hline A(x)-B(x)=& 5x^6-x^5+3x^3\phantom{+3x^2} +x-12\end{aligned}\]](https://www.cursomates.com/wp-content/ql-cache/quicklatex.com-a8b79e5cb27093d9d14c758f88365273_l3.png)
Por supuesto, como te podrás imaginar, la resta de polinomios no es conmutativa. Así si lo que quiero es calcular ![]() tengo que operar de esta manera:
tengo que operar de esta manera:
![Rendered by QuickLaTeX.com \[\begin{aligned} B(x)= & \phantom{-5x^6++}x^5 -5x^3+3x^2 -x+10\\ -A(x)= &-5x^6 \phantom{+..x^5} +2x^3 -3x^2 \phantom{-x+} +2\\\hline B(x)-A(x)=& -5x^6+x^5-3x^3\phantom{+3x^2.}-x+8\end{aligned}\]](https://www.cursomates.com/wp-content/ql-cache/quicklatex.com-564f08a9289bff8d1ab4fb2c0bf24f8c_l3.png)
Como ves no es lo mismo sumar que restar polinomios; y cuando restas quién es el minuendo y quién el sustraendo es muy importante.
Multiplicación de un polinomio por un escalar
Cuando en matemáticas se habla de escalares, lo que se está diciendo es un número. O sea, que en este apartado te voy a enseñar cómo multiplicar monomios por un número. Es muy fácil:

Seguimos con nuestros dos polinomios del ejemplo: ![]() y
y ![]() Ahora vamos a multiplicarlos por un escalar (número):
Ahora vamos a multiplicarlos por un escalar (número):
![]()
Observa cómo he ido multiplicando todos y cada uno de los coeficientes del polinomio por el número 3.
Por otro lado:
![]()
Y así es como se multiplican polinomios por un escalar.
¿Y cómo se divide un polinomio por un escalar? Pues si te sabes aquello de que dividir es multiplicar por el inverso, tendrás claro que dividir por ![]() significa multiplicar por
significa multiplicar por ![]() Así pues:
Así pues:
![]()
Y, al igual que en el producto, los signos de los escalares también tienen su papel en la división:
![]()
Producto de polinomios
Vamos a entrar en algo un poco más serio. Mas serio porque requiere atención.
Cuando explico cómo se multiplican polinomios en clase, siempre hay algún alumno que no suele atender porque… «total ya me lo explicará fulanito» o «es muy fácil» o «ya lo miraré en el libro» o la peor de todas que he oído con estas orejitas que tengo 

Pero volvamos al producto de polinomios. Y continuamos con nuestros viejos amigos ![]() y
y ![]() . Lo que debes hacer es aplicar la propiedad distributiva, lo cual se traduce en multiplicar todos los monomios del primer polinomio por todos los monomios del segundo polinomio.
. Lo que debes hacer es aplicar la propiedad distributiva, lo cual se traduce en multiplicar todos los monomios del primer polinomio por todos los monomios del segundo polinomio.
¿Puedo multiplicarlos en línea? Sí. Pero es algo muy farragoso y bastante tienes con no confundirte, como para añadir una dificultad extra.
Lo que debes hacer es poner los polinomios exactamente igual que cuando te enseñaron a multiplicar números de varias cifras, y luego empezar a multiplicar los monomios UNO POR UNO. Te enseño cómo y luego te lo explico:
![Rendered by QuickLaTeX.com \[\text{ \begin{tabular}{cc ccc ccc ccc} &&&&$5x^6$&&&$-2x^3$&$+3x^2$&&$-2$ \\ &$ $&$ $&$ $&$ $&$ x^5$&$ $&$-5x^3 $&$+3x^2 $&$-x $&$+10 $ \\\hline \\\color{red} &$ $&$ $&$ $&$\color{red}50x^6 $&$ $&$ $&$\color{red}-20x^3 $&$\color{red}+30x^2 $&$ $&$\color{red} -20$ \\ &$ $&$ $&$ $&$ $&$ $&$+2x^4 $&$ -3x^3$&$ $&$+2x $&$ $ \\ &$ $&$15x^8 $&$ $&$ $&$-6x^5 $&$9x^4 $&$ $&$-6x^2 $&$ $&$ $ \\ &$-25x^9 $&$ $&$ $&$+10x^6 $&$-15x^5 $&$ $&$+10x^3 $&$ $&$ $&$ $ \\ $5x^{11}$&$ $&$-2x^8 $&$+3x^7 $&$ $&$-2x^5 $&$ $&$ $&$ $&$ $&$ $ \\\hline\\ $5x^{11}$&$ -25x^9$&$+13x^8 $&$-2x^7 $&$+60x^6 $&$-23x^5 $&$+11x^4 $&$-13x^3 $&$ +24x^2$&$+2x $&$-20 $ \\ \end{tabular}}\]](https://www.cursomates.com/wp-content/ql-cache/quicklatex.com-f50b5fac29c198d7c4b6577d2ac91fe3_l3.png)
Como ves es el mismo algoritmo que cuando multiplicas números, pero ahora lo que tienes que multiplicar son monomios con monomios.
- Date cuenta que cada grado tiene adjudicada una columna: está la columna de los términos independientes, de los términos en
 , de los términos en
, de los términos en  ….
…. - Cuando multipliques es importante que seas muy metódico y que vayas colocando los monomios que te salen en su columna correspondiente.
- El grado del producto es la suma de los grados de los polinomios que se multiplican. En este caso es 11 porque

- Te voy a leer la primera línea de la multiplicación (está escrita en rojo) para que veas cómo se puede ir montando:
- Empiezo con el
 y debo multiplicarlo por cada uno de los monomios que hay en la fila superior (que es nuestro polinomio
y debo multiplicarlo por cada uno de los monomios que hay en la fila superior (que es nuestro polinomio  ).
).  multiplicado por
multiplicado por  es
es  y ¿ves dónde he escrito
y ¿ves dónde he escrito  ? en la columna de los términos independientes.
? en la columna de los términos independientes. multiplicado por
multiplicado por  es
es  y lo coloco en su sitio que es la columna de los términos en
y lo coloco en su sitio que es la columna de los términos en 
 por
por  … exacto, es
… exacto, es  y ¿adivinas qué hago? lo coloco en la columna de los términos en
y ¿adivinas qué hago? lo coloco en la columna de los términos en 
 por
por  da
da  y… ¡¡a la columna de los términos en
y… ¡¡a la columna de los términos en  !!
!!
- Empiezo con el
Pues así como he hecho con la fila que está en rojo debes ir completando cada una de las filas: la de ![]() , la de
, la de ![]() , la de
, la de ![]() y la de
y la de ![]()
Haciéndolo como te he indicado te aseguras dos cosas muy importantes:
- Multiplicas a todos los monomios del primer polinomio por todos los monomios del segundo pero sólo una vez.
- Como has colocado cada monomio según su grado, te aseguras de que al sumarlos no se te olvida ninguno, ni de que no sumas dos que no debías.
Pues así es como se multiplican polinomios. No es algo difícil, pero requiere atención y sobre todo necesitas estar centrado para no saltarte ningún paso.
División de polinomios
Si antes te pareció que la multiplicación de polinomios podría llegar a ser algo compleja, ahora toca la división; y sí te digo que aquí aumenta la dificultad un punto en cómo se realiza.
Vamos a dividir dos polinomios como son ![]() y
y ![]() .
.
Lo primero que debes saber es lo siguiente:
- El dividendo debe tener mayor grado que el divisor. En caso contario la división no puede hacerse.
- La división acaba, por tanto, cuando el grado del dividendo es menor que el divisor.
- El producto de los grados del divisor y el cociente es igual al grado del dividendo.
Así pues, vamos a dividir ![]() Al igual que en el apartado anterior te pongo lo que debes escribir y luego te lo explico.
Al igual que en el apartado anterior te pongo lo que debes escribir y luego te lo explico.
![Rendered by QuickLaTeX.com \[\text{\begin{tabular}{ccccc l} $x^4 $&$ $&$-3x^2 $&$ +5x$&$-2 $&{\hspace*{-7pt}}\vline \hspace*{7pt}$x^2-3x+2 $\\\cline{6-6}\\ $\color{red} -x^4$&$\color{red}+3x^3 $&$\color{red}-2x^2 $&$ $&$ $&$\color{blue}x^2\color{black}+3x+4 $\\\cline{1-5}\\ $ $&$ 3x^3$&$-5x^2 $&$+5x $&$ -2$&$ $\\ $ $&$ -3x^3$&$+9x^2 $&$-6x $&$ $&$ $\\\cline{2-5}\\ $ $&$ $&$ 4x^2$&$ -x$&$ -2$&$ $\\ $ $&$ $&$ -4x^2$&$+12x $&$-8 $&$ $\\\cline{3-5}\\ $ $&$ $&$ $&$ 11x$&$-10 $&$ $\\\end{tabular}}\]](https://www.cursomates.com/wp-content/ql-cache/quicklatex.com-f6bab06cf693d794051e590b3dc55b06_l3.png)
Voy a explicarte qué ha ocurrido aquí:
- Igual que cuando haces una división con números reales, el algoritmo está repartido en dividendo, divisor, cociente y resto.
- Tal y como ha ocurrido en la multiplicación de polinomios, en la parte que hay debajo del dividendo existen columnas que son ocupadas según el grado del monomio en cuestión.
- Te cuento cómo he conseguido calcular la línea del dividendo que está escrita en rojo. Las demás líneas se calculan exactamente igual:
- Empiezo por el
 que está escrito en negro y lo opero con el
que está escrito en negro y lo opero con el  del divisor.
del divisor. - Pienso: «¿
 dividido entre
dividido entre  ?» claramente es
?» claramente es  luego lo escribo en el cociente (azul).
luego lo escribo en el cociente (azul). - Ahora canto lo siguiente:
- «
 (azul) por
(azul) por  es
es  pero lo cambio de signo» y obtengo así el
pero lo cambio de signo» y obtengo así el  que está en rojo.
que está en rojo. - «
 (azul) por
(azul) por  es
es  , y lo cambio de signo» y obtengo el
, y lo cambio de signo» y obtengo el  que está en rojo.
que está en rojo. - «
 (azul) por
(azul) por  es
es  , pero antes de escribirlo lo cambio de signo» y obtengo así el
, pero antes de escribirlo lo cambio de signo» y obtengo así el  que está en rojo.
que está en rojo.
- «
- Una vez que he acabado de multiplicar el
 azul por todo lo que aparece en el divisor y que he conseguido la línea roja, ahora las sumo. ¿qué ocurre? pues que
azul por todo lo que aparece en el divisor y que he conseguido la línea roja, ahora las sumo. ¿qué ocurre? pues que  desaparece (a veces tienes suerte y desaparecen más cosas). Así hemos conseguido rebajar un grado el dividendo
desaparece (a veces tienes suerte y desaparecen más cosas). Así hemos conseguido rebajar un grado el dividendo
- Empiezo por el
- Una vez que he conseguido rebajar un grado el dividendo continúo haciendo lo mismo ¿hasta cuándo? Hasta que me quede un polinomio de grado menor que el divisor: en este caso
 . En este momento paro la división.
. En este momento paro la división.
Y por último ¿qué te queda por hacer? Pues queda nombrar cada cosa que has ido calculando:
- Dividendo:

- Divisor:

- Cociente:

- Resto:

Y unas cuantas preguntas más:
- ¿Cómo podemos saber que no nos hemos confundido? pues porque como en cualquier división, el Dividendo es igual al divisor multiplicado por el cociente más el resto [
 ]. Es decir, debes comprobar que:
]. Es decir, debes comprobar que: ![Rendered by QuickLaTeX.com \[x^4-3x^2+5x-2=\left(x^2-3x+2)\cdot (x^2+3x+4)+(11x-10)\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIzOTUiIGhlaWdodD0iMjAiIHZpZXdCb3g9IjAgMCAzOTUgMjAiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIGZpbGw9IiNjZmQ0ZGIiLz48L3N2Zz4=)
- ¿Y si el resto es 0? En ese caso has conseguido una división exacta y significa que el divisor es un factor el dividendo. Pero esto es otra entrada.
- ¿Siempre el cociente y el divisor tienen el mismo grado? No. En este caso ha sido del mismo grado pero no tiene por qué. Lo que sí ocurre siempre es que la suma de los grados del divisor y el cociente es igual al grado del dividendo (esto es un truco para saber rápidamente si te has confundido).
- ¿Los coeficientes directores del dividendo y el cociente coinciden? Tampoco hay una razón para que coincidan, ya que el coeficiente director de cociente depende tanto del dividendo como del divisor.
Ejercicios típicos de exámenes
A continuación te pongo uno de los ejercicios sobre polinomios que he ido solicitando a mis alumnos a lo largo del tiempo. Como verás en una sola pregunta aparece todo (suma o resta de polinomios, producto de polinomios por escalares y producto de polinomios).
Dados los siguientes polinomios: ![]() ,
, ![]() y
y ![]() , calcula
, calcula ![]()
Mi consejo para resolver este tipo de problemas es que vayas haciendo las cosas poco a poco. Lo más complicado, en mi opinión es la multiplicación de polinomios, así que yo empezaría por ahí, y una vez hecha escribiría el resultado para que no se me olvide:
![]()
Después yo optaría por calcular cuánto es ![]() (con el signo menos y todo):
(con el signo menos y todo):
![]()
Y una vez que lo tengo así, personalmente, yo te aconsejo que lo pongas de la siguiente manera y sumes:
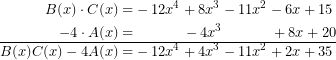
Creo que es muy interesante no sólo hacer las cosas bien, si no ser elegante. Y tu profe, que no te tiene manía agradecerá que resuelvas los ejercicios de esta manera.
En resumen
Espero que con esta entrada te haya quedado claro cómo operar con polinomios en cuanto a sus operaciones básicas como son la suma, resta, multiplicación y división.
Ya te he dicho que esta entrada es la continuación de la dedicada a los monomios; y que si quieres continuar con este tema puedes leer las entradas sobre la factorización de polinomios y la regla de Ruffini.

Si quieres contactar conmigo puedes hacerlo aquí
Si te gusta lo que hago y quieres invitarme a un café 
Bibliografía
- Aparicio Peñas, A. M., Arribas Ruiz, F., González García, C., Llorente Medrano, J., Ruiz Jiménez, M.; 2015; Matemáticas aplicadas a las ciencias sociales (I); Ed. Editex; Madrid; ISBN: 978-84-9078-504-1.
- Argüeso, M., Borobia, N., Lázaro, O., Pajares, A., Tomeo, V.; 2015; Matemáticas aplicadas a las ciencias sociales I; Ed. Paraninfo; Madrid; ISBN: 978-84-283-3548-5.
- Colera Jiménez, J., Oliveira González, M. J., Gaztelu Albero, I., Colera Cañas, R.; 2016; Matemáticas orientadas a las enseñanzas académicas: 4 ESO; Ed. Anaya; Madrid; ISBN: 978-84-698-1069-9.
Vida de la entrada:
– 2020-11-05: Publicación.
–

 o cosas peores que he llegado a ver
o cosas peores que he llegado a ver  . Si haces tal cosa, y en función de en qué curso estés; tu profe, que no te tiene manía, va a penalizarte o a anularte toda la pregunta del examen.
. Si haces tal cosa, y en función de en qué curso estés; tu profe, que no te tiene manía, va a penalizarte o a anularte toda la pregunta del examen. Ya sabes, aquellos coeficientes, exponentes o monomios enteros que están escondidos: no los ves pero debes tenerlos en cuenta. Puedes estar seguro de que aparecerán varias veces a lo largo de un solo ejercicio.
Ya sabes, aquellos coeficientes, exponentes o monomios enteros que están escondidos: no los ves pero debes tenerlos en cuenta. Puedes estar seguro de que aparecerán varias veces a lo largo de un solo ejercicio.

