▶ 🚩 Más sobre polinomios 🎖

¿Polinomios otra vez? ¿de verdad que son tan importantes? Bueno pues sí. Hay libros y libros que hablan sobre ellos y ahí están dando la barrila.

En esta entrada te voy a contar cosas que no se suelen contar en clase de ESO y Bachillerato sobre polinomios, porque no vienen en el temario y porque tampoco hay tiempo para verlo. Además creo que si algunas de las cosas que te voy a decir se contaran en enseñanza media a alguien le estallaba la cabeza… (posiblemente al profesor).

Te voy a explicar qué son las fórmulas de Cardano-Vieta y cómo hallar las raíces de polinomios palíndromos (que son un tipo muy especial de polinomios)

[latexpage]

Cosas que no te van a contar sobre polinomios

Lo que te voy a contar en esta entrada sobre polinomios, jamás lo he contado en una clase de ESO o bachillerato, y jamás lo haré. Sin embargo, para mi, es muy interesante porque relaciona varias áreas de las matemáticas, y sobre todo porque muestra la importancia de pensar una estrategia ganadora. Además, el blog lo redacto yo y me apetece

La mayoría de lo que te voy a contar a continuación lo he sacado de los libros de Suprún y Godement que te dejo en la bibliografía. Además el libro de de Diego es excelente. Pero los problemas que te propongo son de cosecha propia.

Fórmulas de Cardano-Vieta

Cuando aprendes a factorizar polinomios, digamos que por la regla de Ruffini, al final debes escribir su factorización de la siguiente manera:

$$P(x)=a_n(x-r_n)\cdot(x-r_{n-1})\cdots(x-r_2)\cdot(x-r_1)$$

Es incluso posible que tu profe, que no te tiene manía te haya hablado de la multiplicidad de las raíces y que, por ejemplo, puedes escribir $$P(x)=(x-3)^3\cdot(x-1)\cdot(x+2)$$ en lugar de $$P(x)=(x-3)\cdot(x-3)\cdot(x-3)\cdot(x-1)\cdot(x+2)$$

Incluso, hasta es posible que te hayas encontrado a tu profe ante una ecuación de segundo grado como $x^2-9x+18=0$ decirte nada más ver la ecuación:

Las soluciones son $x=6$ y $x=3$

Bueno, pues todo esto (sobre todo lo de la ecuación de segundo grado que te acabo de decir) tiene que ver con las fórmulas de Cardano-Vieta.

Partimos del polinomio factorizado anterior $P(x)=a_n(x-r_n)\cdot(x-r_{n-1})\cdots(x-r_2)\cdot(x-r_1)$, pero si lo desarrollamnos tenemos

$$P(x)=a_n(x-r_n)\cdot(x-r_{n-1})\cdots(x-r_2)\cdot(x-r_1)=a_nx^n+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\cdots+a_2x^2+a_1x+a_0$$

¿Hay alguna manera de poner en relación el coeficiente del polinomio desarrollado con las raíces del polinomio factorizado? Pues sí. Vamos a verlo:

Relación entre las raíces y los coeficientes de un polinomio:

Puedes entretenerte en hacer un montón de operaciones e ir desarrollando un polinomio de grado $n$. Pero al final tendrás lo que te pongo en la siguiente lista. Para elaborarla he considerado que todas las raíces son distintas, es decir, si una raíz tiene multiplicidad 2 la pongo 2 veces y así sucesivamente:

• $\displaystyle \frac{a_{n-1}}{a_n}=-\left(r_1+r_2+\cdots +r_n\right)$ Es decir, el coeficiente del término en $x^{n-1}$ dividido por el coeficiente director, es igual a la suma de raíces del polinomio.
• $\displaystyle \frac{a_{n-2}}{a_n}=r_1\cdot r_2+r_1\cdot r_3+\cdots+ r_1 \cdot r_n+ r_2 \cdot r_3+\cdots +r_2\cdot r_n+\cdots \cdots r_{n-1}\cdot r_n$ Es decir, que el segundo coeficiente de un polinomio (el de $x^{n-2}$) dividido por el coeficiente director del polinomio, es la suma del producto de las raíces de dos en dos pero cambiado de signo.
• $\displaystyle \frac{a_{n-3}}{a_n}=-\left(r_1\cdot r_2\cdot r_3+r_1\cdot r_2\cdot r_4+\cdots +r_{n-2}\cdot r_{n-1}\cdot r_n\right)$ Observa que ahora sumamos el producto de las raíces del polinomio, tomadas de tres en tres.
• …
• Y así continuamos hasta llegar a
• …
• $\displaystyle \frac{a_0}{a_n}=(-1)^n\cdot r_1\cdot r_2\cdots r_n$ Es decir, el término independiente dividido entre el coeficiente director, es el producto de todas las raíces, y su signo depende del grado del polinomio.

¿Te parece complicado? No lo es tanto. Fíjate que ocurre cuanto en clase te dicen , nada más ver la ecuación $x^2-9x+18=0$ que sus soluciones son $x=3$ y $x=6$.

¿Cómo lo sabe tu profe, que no te tiene manía?

Tu profe sabe que en la enseñanza media todas las ecuaciones, polinomios y ejercicios están pensados y repensados, y cuando trabajas con polinomios ocurre lo siguiente (y hallar las soluciones de una ecuación es equivalente a hallar las raíces de un polinomio de grado dos):

1. El coeficiente director es 1
2. Lo más seguro es que las soluciones sean números enteros.
3. Por el teorema del factor sabes que las raíces enteras de los polinomios son divisores del término independiente.
4. Por las fórmulas de Cardano Vieta que acabamos de ver, la suma de las raíces cambiadas de signo, es el número que acompaña a la $x$. Es decir es el coeficiente de $x$.
5. Tu profe hace un cálculo rápido y dice:
   1. Divisores de 18: $D(18)=\{\pm1,\pm2,\pm3\pm6,\pm9,\pm18\}$
   2. ¿Cuáles suman 9? $9=3+6$
   3. Pues ya tengo las soluciones $x_1=3$ y $x_2=6$

¿Yo lo uso? Sí, lo uso, pero no me tiro a la piscina. Quiero decir que al final siempre resuelvo la ecuación de segundo grado, y entonces ¿para qué quieres las fórmulas de Cardano-Vieta? Porque me dan pistas de cuáles van a ser las soluciones, pero no me fío de haber calculado el signo correctamente (sobre todo después de una semana a 5h diarias de clase ); así que en el caso anterior yo diría: las soluciones van a estar con 3 y 6, pueden ser (3,6), (-3,6), (3,-6) o(-3,-6) Si resuelvo la ecuación de segundo grado y no sale una de estas cuatro es que me he confundido y debo repasar. Además una vez que tienes la ecuación resuelta, puedes comprobarla muy fácilmente:

1. Multiplicas tus raíces: Te debe salir el término independiente.
2. Sumas tus raíces: Te debe salir el coeficiente de $x$ pero con el signo cambiado.
3. ¡¡Has visto que fácil es ver si has hecho bien una ecuación de segundo grado??

Convéncete que esta es una de las formas más inteligentes de usar las fórmulas de Cardano-Vieta. Con esas cuatro parejas de soluciones, puedo proponerte las siguientes ecuaciones, y lo que yo te propongo es que uses las fórmulas Cardano-Vieta para «acotar» el conjunto de posibles soluciones a estudiar:

$$x^2-9x+18=0$$ $$x^2-3x-18=0$$ $$x^2+3x-18=0$$ $$x^2+9x+18=0$$

Polinomios palíndromos

Seguro que conoces palabras palíndromas como «oso, reconocer, somos» y también te sabrás alguna oración de este tipo como «dábale arroz a la zorra el abad» o «Roma ni se conoce sin oro, ni se conoce sin amor». Son oraciones o palabras que se leen igual de izquierda a derecha que de derecha a izquierda.

Vale, bien, y ¿qué tiene que ver esto con los polinomios? Pues que un polinomio puede ser palíndromo si los coeficientes se disponen de manera especial, y siempre nos vamos a ocupar de factorizarlos. Por ejemplo, imagínate que queremos factorizar los siguiente polinomios:

• $\displaystyle P(x)= 3x^4+2x^3-x^2+2x+3$
• $\displaystyle P(x)= 4x^6-2x^5-x^4+x^3-x^2-2x+4$ La factorización de este polinomio es diabólica lo dejamos para el final del final de la entrada.
• $\displaystyle P(x)= x^6-3x^5+2x^4-3x^3+2x^2-3x+1$
• $\displaystyle P(x)= -3x^6+6x^5+18x^4-12x^3-18x^2+6x+3$

Todos estos polinomios tienen en común que los coeficientes son simétricos, es decir, son de la forma $ABCCBA$ o $ABCDCBA$ o alguna otra similar. Ya veremos que también se puede jugar con los signos.

Finalmente, hay polinomios que se pueden transformar a palíndromos con un «poco» de ingenio como:

• $P(x)= 6x^3-x^2-20x+12$
• $\displaystyle P(x)= x^3-2x^2-2x+1$

Puedes intentar factorizarlos. No vas a poder, porque lo más seguro (bueno, en estos casos que te he puesto es seguro) es que las raíces no sean enteras, y a ver cómo encuentras tú las raíces no enteras de un polinomio de grado 3, 4, 5, 6… Es verdad que la cúbica y la cuártica tienen fórmulas que las resuelven (a modo de la ecuación de segundo grado), pero ¿quién se las sabe? además Galois ya demostró que a partir de 5 grado es inútil buscar una fórmula que la resuelva. No existe.

Puedes intentar aplicar el teorema de Bolzano e ir acotando las soluciones. Es más, puedes aplicar métodos de cálculo numérico, como el de Newton-Raphson e intentar tener una aproximación tan buena como desees de la solución. Pero nosotros aquí vamos a calcular la solución exacta. ¡¡HEMOS VENIDO A JUGAR!!

Cómo enfrentarte a un polinomio palíndromo

Ante todo tranquilidad.

• Lo primero es comprobar que la solución no es $x=0$. Esto nos va a facilitar poder dividir como te indico a continuación.
• Si $x=0$ es raíz del polinomio, entonces es porque no posee término independiente, y podrás sacar factor común una potencia de $x$.
• Al final debes haber conseguido un polinomio con término independiente y con coeficientes dispuestos de manera capicúa.
• Ahora debes contar el grado del polinomio. Si es par todo va bien, pero si es impar, eso significa que hay un número par de monomios, por lo que vas a tener que multiplicar tu polinomio por $(x+\alpha)$.
• Al final, se trata de conseguir un número impar de monomios y cuyos coeficientes se dispongan de manera capicúa.
• Lo siguiente es dividir por la potencia de $x$ central (por esto necesitábamos que $x=0$ no fuese solución). Así el polinomio queda convertido en $(MONOMIOS)\ +\ (COEFICIENTE\ CENTRAL)\ +\ (FRACCIONES\ ALGEBRAICAS)$
• El último paso es hacer un cambio de variable e ir ajustando la ecuación que nos va a ir saliendo.
• Y como siempre, precaución de no confundirse que es muy, pero que muy fácil.

Y como es posible que la lista anterior te haya dejado igual que al principio vamos a ir empezando con ejemplos. Te voy a poner los ejemplos en orden creciente de dificultad (al menos lo que yo considero orden creciente de dificultad); pero me puedes dejar en comentarios si crees que otro orden iría mejor.

¡¡Ah!! También me puedes dejar en comentarios otros ejemplos que se te ocurran. Pero por favor, antes de lanzarte a la piscina mira a ver si tiene agua e intenta resolverlos

Ejemplo 1. Factoriza el siguiente polinomio

$$\displaystyle P(x)= 2x^4+9x^3+14x^2+9x+2$$

En este caso el procedimiento es sencillo. Debemos hallar las soluciones (raíces) de la ecuación $x^4+9x^3+14x^2+9x+2=0$. Lo primero es ver que efectivamente la solución no es $x=0$, así pues podemos hacer lo siguiente:

1.-Dividimos por $x^2$. Si quieres puedes decir que es el monomio mediana del polinomio porque deja igual número de monomios a su izquierda y a su derecha.

$$2x^2+9x+14+\frac{9}{x}+\frac{2}{x^2}=0$$

2.- Ahora hacemos un cambio de variable:

$$y=x+\frac{1}{x}\Longrightarrow x=\frac{y\pm\sqrt{y^2-4}}{2}$$

Este el el TRUCAZO. El cambio de variable es la equis sumada a su inversa $\displaystyle y=x+\frac{1}{x}$ (¿Comprendes ahora por qué te dije que nunca lo contaré en una clase de ESO o bachillerato? pues espera los siguientes ejemplos…?)

3.-Calculamos $y^2$

$$y^2= x^2+2+\frac{1}{x^2}$$

4.- Vamos a transformar nuestra ecuación en $x$ en una ecuación de segundo grado en $y$. Te pongo el cambio ya hecho, espero que no tengas problemas para ver qué he hecho; si no es así, déjamelo escrito en comentarios.

$$2y^2+9y+10=0$$

5.- Calculamos las soluciones de esta nueva ecuación:

$$\left\{\begin{aligned}\displaystyle y_1&=-2\\ \displaystyle y_2&=-\frac{5}{2}\end{aligned}\right.$$

6.- Deshacemos el cambio y calculamos los valores de $x$. Igual que antes, yo ya te doy las soluciones y dejo que las operaciones corran de tu cuenta. Pero si tienes algún problema en este paso, dímelo en comentarios …

$$\left\{\begin{aligned}
x_1&=\displaystyle -\frac{1}{2}\\
x_2&=-2\\
x_3&=-1\ \text{(solución doble)}\\
\end{aligned}\right.$$

Como ves las soluciones han salido bastante amigables, pero lo normal es que ya en la ecuación en $y$ empiecen a salir soluciones que… bueno, soluciones no muy agradables. Voy a ponerte la factorización del polinomio.

$$P(x)=2(x+1)^2\cdot \left(x+\frac{1}{2}\right)\cdot (x+2)$$

Ejemplo 2. Factoriza el siguiente polinomio

$$\displaystyle P(x)= x^6-3x^5+2x^4-3x^3+2x^2-3x+1$$

El proceso que debemos seguir es el mismo que antes:

1.- Para factorizar el polinomio anterior tenemos que hallar las raíces de la ecuación $x^6-3x^5+2x^4-3x^3+2x^2-3x+1=0$

2.- Comprobamos que $x=0$ no es solución de la ecuación anterior.

3.- Dividimos por $x^3$

$$x^3 -3x^2+2x-3 +\frac{2}{x} -\frac{3}{x^2}+1=0$$

4.- El trucazo, como antes, es hacer el cambio $\displaystyle y=x+\frac{1}{x}$ y hallar $y^2$ e $y^3$

• $\displaystyle y^2= x^2+2+\frac{1}{x^2} \Longrightarrow x^2+\frac{1}{x^2}= y^2-2$
• $\displaystyle y^3= x^3+3x+\frac{3}{x}+\frac{1}{x^3}\Longrightarrow x^3+\frac{1}{x^3}= y^3-3y$

5.- Transformamos nuestra ecuación en $x$ a una ecuación cúbica en $y$

$$y^3-3y^2-y+3=0$$

6.- Hallamos las soluciones de esta ecuación (en este caso por Ruffini salen perfectamente)

$$\begin{aligned}y_{1,2}&=\pm 1\\y_3&=3\end{aligned}$$

7.- Deshacemos el cambio para cada una de las soluciones (y aquí te vas a tener que pelear con los números complejos en cuatro de las soluciones)

$$\displaystyle y_1=1\Longrightarrow 1=x+\frac{1}{x} \longrightarrow \left\{ \begin{aligned} x_1 & = \frac{1}{2}+ \frac{1}{2} \sqrt{3}i \\ x_2 & = \frac{1}{2}- \frac{1}{2} \sqrt{3}i \end{aligned}\right.$$

$$\displaystyle y_2=-1\Longrightarrow -1=x+\frac{1}{x} \longrightarrow \left\{ \begin{aligned} x_3 & = -\frac{1}{2}+\frac{1}{2} \sqrt{3}i \\ x_4 & = -\frac{1}{2}- \frac{1}{2} \sqrt{3}i \end{aligned}\right.$$

$$\displaystyle y_3=3\Longrightarrow 3=x+\frac{1}{x} \longrightarrow \left\{ \begin{aligned} x_5 & = \frac{3}{2}+ \frac{1}{2} \sqrt{5} \\ x_6 & = \frac{3}{2}- \frac{1}{2} \sqrt{5} \end{aligned}\right.$$

¡¡Qué?? ¿¿Te pensabas que iba a ser todo coser y cantar!! Ya te dije que aquí habíamos venido a jugar, y es normal que aparezcan números complejos…

Pero ten en cuenta una cosa. Ya te he comentado en una entrada anterior que el Teorema Fundamental del Álgebra indica que todo polinomio con coeficientes complejos de grado $n$ posee $n$ raíces complejas; y eso es exactamente lo que ha pasado: partíamos de un polinomio de grado 6 y hemos hallado 6 soluciones.

Vamos con la factorización del polinomio, pero no te voy a poner números complejos si no un par de polinomios de grado dos (de donde sacas las raíces complejas).

$$P(x)= \left(x^2-x+1\right)\cdot \left(x^2+x+1\right)\cdot \left(x-\left(\frac{3}{2}+ \frac{1}{2} \sqrt{5}\right)\right)\cdot\left(x- \left(\frac{3}{2}- \frac{1}{2} \sqrt{5}\right)\right)$$

Ejemplo 3. Factoriza el siguiente polinomio

$$\displaystyle P(x)= -3x^6+6x^5+18x^4-12x^3-18x^2+6x+3$$

En este caso seguimos como antes. Este es el último ejemplo de este tipo que te voy a poner, el siguiente polinomio tendremos que «ajustarlo».

Como en casos anteriores, para ver si podemos factorizar este polinomio palindrómico, comprobamos que $x\neq 0$. Como es verdad, que el 0 no es raíz del polinomio empezamos:

1.- Para factorizar el anterior polinomio, tenemos que encontrar las raíces de $-3x^6+6x^5+18x^4-12x^3-18x^2+6x+3=0$

2.- Como $x=0$ no es raíz del polinomio, procedemos a dividirlo por el la $x$ del monomio central. En este caso dividimos por $x^3$

$$-3x^3+6x^2+18x-12-\frac{18}{x}-\frac{6}{x^2}+\frac{3}{x}=0$$

Observa ahora que los coeficientes del siguen el patrón $ABCDCBA$ pero los signos se alternan. Esto va a influir en el cambio de variable que vamos a hacer.

3.- Hacemos el cambio $\displaystyle y=x-\frac{1}{x}$. Fíjate que ahora resto la inversa. Hallo su cuadrado y su cubo:

$$y^2= x^2-2+\frac{1}{x^2}$$

$$y^3=x^3-3x+\frac{3}{x}-\frac{1}{x^3}$$

4.- Ajustamos el cambio de variable para pasar de tener una ecuación en $x$ de grado 6 a tener una ecuación en $y$ de grado 3.

$$-3y^3+6y^2+9y=0$$

5.- Resolvemos esta ecuación cúbica, que por suerte es sencilla de resolver :

$$-3y\left(y^2-2y+3\right)=0\Longrightarrow \left\{\begin{aligned}y_1&=0\\
y_2&=3\\
y_3&=-1\end{aligned}\right.$$

6.- Toca deshacer el cambio:

$\displaystyle y=0=x-\frac{1}{x}\quad\Longleftrightarrow \quad\left\{\begin{aligned}x_1&=+1\\x_2&=-1\end{aligned}\right.$

$\displaystyle y=-1=x-\frac{1}{x} \quad \Longleftrightarrow\quad\left\{\begin{aligned}x_3&=\frac{-1+\sqrt{5}}{2}\\x_4&=\frac{-1-\sqrt{5}}{2}\end{aligned}\right.$

$\displaystyle y=3=x-\frac{1}{x}\quad \Longleftrightarrow \quad\left\{\begin{aligned}x_5&=\frac{3+\sqrt{13}}{2}\\x_6&=\frac{3+\sqrt{13}}{2}\end{aligned}\right.$

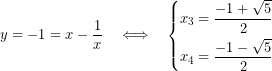
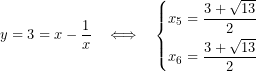
Me he saltado algunos pasos porque bueno… si has llegado hasta aquí supongo que no tendrás problema para averiguarlos: resolver una ecuación de segundo grado por aquí, hallar un factor común por allá…

Y como de costumbre, de una ecuación de sexto grado, obtenemos seis soluciones diferentes.

Vamos con la factorización del polinomio. Pero al igual que antes te voy a poner una factorización un poco sui generis y pondré algunos factores que sean polinomios de grado dos. No es la forma canónica de hacerlo, pero creo que queda más inteligible (y si no echa un vistazo a la factorización del Ejemplo 1):

$$P(x)= \left(x-1 \rigth)\cdot\left(x +1\rigth)\cdot\left(x^2+x-1 \rigth)\cdot\left(x^2-3x-1 \rigth) $$

Ejemplo 4. Factoriza el siguiente polinomio

$$\displaystyle P(x)= x^3-2x^2-2x+1$$

Lo primero que debo decirte, es que este polinomio (y su ecuación cúbica asociada) se resuelven de forma muy sencilla por Ruffini; pero te lo he puesto aquí para que veas otra manera de resolverlo. Es verdad que lo que vamos a hacer ahora es dar una vuelta muy grande, tanto como ir de Madrid a Sevilla pasando primero por Berlín; pero creo que es una buena forma de acercarse a esta manera de resolver polinomios.

Como te digo, si lo haces por Ruffini, las soluciones son $\displaystyle x_1=-1; \quad x_2=\frac{3+\sqrt{5}}{2}; \quad x_3=\frac{3-\sqrt{5}}{2}$. Pero vamos a transformar el anterior polinomio en uno que sea palíndromo.

$$\displaystyle (x^3-2x^2-2x+1)\cdot (x-\alpha)$$

Si desarrollas este producto, obtienes:

$$x^4+(-2-\alpha)x^3+(2\alpha-2)x^2+(2\alpha+1)x-\alpha=\color{red} Ax^4+Bx^3+Cx^2+Bx+A$$

Sin más que igualando coeficientes de ambos polinomios puedes llegar a la conclusión de que $\alpha=-1$

De esta manera, para conseguir la factorización de ese polinomio, debemos resolver la siguiente ecuación.:

$$x^4-x^3-4x^2-x+1=0$$

Como $x\neq 0$ podemos dividirlo todo por $x^2$ y obtenemos:

$$x^2-x-4-\frac{1}{x}+\frac{1}{x^2}=0$$

Y ahora estamos en terreno conocido. El cambio a hacer es $\displaystyle y=x+\frac{1}{x}$ y calculamos $\displaystyle y^2=x^2+2+\frac{1}{x^2}$

Con todo esto podemos transformar nuestra ecuación de cuarto grado en $x$ en una ecuación de grado 2 en $y$:

$$y^2-y-6=0$$

Cuyas soluciones, si aplicas las fórmulas de Cardano-Vieta son: $y_1=3; \ y_2=-2$

Ya sólo queda deshacer el cambio:

$\displaystyle y_1=3\ \Longrightarrow \ \left\{\begin{aligned} x_1&=\frac{3+\sqrt{5}}{2}\\ x_2&=\frac{3-\sqrt{5}}{2} \end{aligned}\right. $

$\displaystyle y_2=-2\ \Longrightarrow \ x_3=-1\ \text{(doble)}$

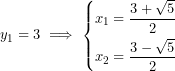
Como ves, resolver así este tipo de polinomios es complicado y es fácil acabar confundiéndote. Pero aún así todavía no hemos acabado.

Nuestro polinomio de partida tiene grado 3, y nosotros hemos hallando las raíces de un polinomio de grado 4, por lo tanto hay alguna solución que no nos vale ¿cuál? Pues claramente la que introdujimos cuando hicimos la multiplicación de los polinomios $P(x)$ y $(x-\alpha)$. Es decir, una de las soluciones de $x=-1$ es espuria y debemos eliminarla.

$$P(x)=\left(x-\frac{3+\sqrt{5}}{2}\right)\cdot\left(x-\frac{3-\sqrt{5}}{2}\right)\cdot \left(x+1\right)$$

Ejemplo 5. Factoriza el siguiente polinomio

$$P(x)= 6x^3-x^2-20x+12$$

Como este polinomio tiene grado impar, eso significa que tiene un número par de monomios y por tanto debemos multiplicarlo por $(x+\alpha)$ para conseguir un polinomio con un grado par de monomios.

Atención:

1. Yo lo he multiplicado por $(x+\alpha)$, pero podría haberlo hecho por $(x-\alpha)$. Sólo es cuestión de ajustar los signos.
2. Cuando multiplico, estoy introduciendo una solución espúrea del polinomio, que al final deberé limpiar.

El caso es que lo que debemos hacer es:

$$\left(6x^3-x^2-20x+12\right)\cdot \left(x+\alpha\right)=0$$

Si haces cuentas obtienes lo siguiente:

$$6x^4+(6\alpha-1)x^3+(-20-\alpha)x^2+(12-20\alpha)x+12\alpha=0$$

Y ahora debes preguntarte que tu ecuación debe tener la siguiente forma:

$$Ax^4+Bx^3+Cx^2+Bx+A=0$$

Por lo que, igualando coeficientes, obtenemos:

• $A=6=12\alpha\ \Longrightarrow\ \alpha=1/2$
• $B=6\alpha-1=12-20\alpha\ \Longrightarrow\ \alpha=1/2$
• $\displaystyle C=-20-\alpha=-20-\frac{1}{2}=\frac{-41}{2}$

Así pues, ya tenemos nuestros coeficientes calculados y resulta que el polinomio a factorizar (o lo que es equivalente, la ecuación a resolver) es:

$$6x^4+2x^3-\frac{41}{2}x^2+2x+6=0$$

Antes de seguir adelante, voy a multiplicar toda la ecuación por 2 y así me evito una fracción. Bastantes complicaciones tenemos ya, como para tener que estar pendiente de un denominador….

$$12x^4+4x^3-41x^2+3x+12=0$$

Pero tú ya eres todo un experto en estas lides y ya sabes que puesto que en este polinomio $x\neq 0$ podemos dividir por $x^2$ y operar:

$$12x^2+4x-41+\frac{4}{x}+\frac{12}{x^2}=0$$

Con el cambio $\displaystyle y=x+\frac{1}{x}$ y $\display y^2=x^2+2+\frac{1}{x^2}$ tenemos que podemos transformar la ecuación anterior en

$$12y^2+4y-65=0$$

Supongo que esta ecuación de segundo grado ya no tiene ningún secreto para ti y sus soluciones son:

• $\displaystyle y_1=\frac{13}{6}$
• $\displaystyle y_1=-\frac{5}{2}$

Por lo que ahora sólo resta deshacer el cambio que es:

$\displaystyle y_1=\frac{13}{6}\ \Longrightarrow \ \left\{\begin{aligned} x_1&=\frac{3}{2}=1.5\\ x_2&=\frac{2}{3}=0.\bar{6} \end{aligned}\right. $

$\displaystyle y_2=-\frac{5}{2}\ \Longrightarrow \ \left\{\begin{aligned} x_3&=-\frac{1}{2}=1.5\\ x_4&=-2 \end{aligned}\right. $

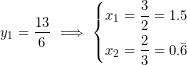
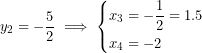
Así que estas son las soluciones de mi polinomio…. PARA ¿Te acuerdas que habíamos introducido una solución cuando multiplicamos por $(x+\alpha)=(x+1/2)$? Pues esa solución hay que quitarla. Por lo que las soluciones a nuestra ecuación (que podemos utilizar para factorizar el polinomio) son:

$$x_1=\frac{3}{2}\qquad\ x_2=\frac{2}{3}\qquad \ x_3=-2$$

Y la factorización del polinomio es:

$$P(x)=6\left(x -\frac{3}{2}\right)\cdot\left(x -\frac{2}{3}\right)\cdot\left(x +2\right)$$

Una pregunta para los comentarios

Según escribo estas lineas sobre este problema se me está ocurriendo que se podría intentar resolver este tipo de problema de polinomios mediante las siguientes cuestiones de análisis matemático: te las voy a esbozar simplemente, pues requiere de un estudio más profundo y espero que me lo vayas dejando en comentarios. En esencia es lo siguiente:

Lo primero que he hecho ha sido hacer un gráfico en R del polinomio en cuestión con el siguiente código:

f01<-function(x){6x^3-x^2-20x+12}
curve(f01, xlim=c(-3,3), ylim=c(-10,30),lwd=, 
     main="Representacion gráfica", xlab="", ylab="")
text(-1, 30, expression(f(x) == 6x^3-x^2-20x+12 ),lwd=2, 
     col="black", cex=1.4)
abline(h=0, col=2, lty="dashed", lwd=2)

De esta manera se obtiene la siguiente representación:

Como ves su gráfica es bastante simétrica (y es aquí donde se da un salto sin red). Así que se podrían hallar las coordenadas del máximo y mínimo y con sus ordenadas ponderar de alguna manera la coordenada de la $x$ donde se corta al eje $X$.

Pero este problema no te lo resuelvo, pues en esta entrada quiero hablar de métodos de álgebra, no de análisis matemático. Te lo dejo a ti. Es tu turno en comentarios: ¿Se podría hacer? ¿Qué requisitos debería reunir la función? ¿Podríamos desplazar la representación de la función por el plano hasta conseguir lo que queremos?

Como pista te digo que el punto de inflexión de esta gráfica es su centro de simetría… ahí queda eso. ¿Aceptas el reto? ¿Recoges el guante?

Ejemplo 6. Factoriza el siguiente polinomio… si te atreves

$$P(x)= 4x^6-2x^5-x^4+x^3-x^2-2x+4$$

¿Creías que me había olvidado de este? Pues no, pero prepárate para enfrentarte a dos cambios de variable y la resolución de una ecuación cúbica. Primero transformaremos la ecuación asociada al polinomio en una cúbica mediante un cambio de variable y luego necesitamos la transformación de Tschirnhaus para su resolución. ¡¡¡Agárrate que vienen curvas!!!! 🔀↪🔁↩🔄⤴🔃⤵

Pero no te preocupes, como es posible que el día que estés leyendo esto aún no haya tenido tiempo de publicar la resolución de la cúbica, te voy a dar todas las estrategias para resolver este polinomio (Sí, aunque parezca mentira el día que escribo estas letras tengo 254 entradas previstas y 54 borradores activos pero sólo 39 publicaciones. Lo siento, no doy más de mí ).

Crucemos los dedos para no confundirnos en ningún paso.

Cambiamos una ecuación de sexto grado en $x$ por una ecuación cúbica en $y$:

Como en los casos anteriores lo primero que tenemos que hacer es un cambio de variable en el polinomio $P(x)= 4x^6-2x^5-x^4+x^3-x^2-2x+4$ que nos permita bajar el grado de esta ecuación (hasta una cúbica). Para ello trabajamos con la ecuación asociada del polinomio $$ 4x^6-2x^5-x^4+x^3-x^2-2x+4=0$$

1.- Comprobamos que $x=0$ NO es solución.

2.- Dividimos por $x^3$ y obtenemos

$$4x^3-2x^2-x+1-\frac{1}{x}-\frac{2}{x^2}+\frac{4}{x^3}=0$$

3.- Hacemos el cambio $\displaystyle y=x+\frac{1}{x}$ y hallamos su cuadrado y su cubo.

$$\begin{aligned}y&=x+\frac{1}{x} \\ y^2&=x^2+2+\frac{1}{x^2} \\ y^3&=x^3+3x+\frac{3}{x}+\frac{1}{x^3} \end{aligned}$$

4.- Ajustamos la ecuación a nuestra variable y así transformamos una ecuación en $x$ de grado 6 en una ecuación cúbica en $y$:

$$4y^3-2y^2-13y+5=0$$

Con lo que ahora queda enfrentarse a una cúbica

Pasemos a enfrentarnos a una cúbica

Debemos pelearnos con esta ecuación:

$$4y^3-2y^2-13y+5=0$$

1.- Para ello, empiezo con la transformación de Tschirnhaus específica de esta ecuación que es:

$\displaystyle t=y+\frac{-2}{3\cdot 4}=y-\frac{1}{6}\longrightarrow y=t+\frac{1}{6}$

2.- Así que hago este cambio de variable y tenemos:

$$4\left(t+\frac{1}{6}\right)^3 -2\left(t+\frac{1}{6}\right)^2-13 \left(t+\frac{1}{6}\right)+5=0$$

3.- Opero y simplifico:

$$4t^3-\frac{163}{12}t-\frac{623}{216}=0$$

¡Qué? ¡Cómo se te va quedando el cuerpo? Pues espérate que aún no ha llegado lo mejor:

4.- Caclulamos el discriminante de esta ecuación cúbica incompleta que es, para la ecuación $a_3x^3+a_1x+a_0=0$: $\displaystyle \Delta =\left(\frac{a_1}{3}\right)^3+\left(\frac{a_0}{2}\right)^2$

$$\Delta= \left(\frac{\displaystyle \frac{-163}{12}}{3}\right)^3+\left(\frac{\displaystyle \frac{-623}{216}}{2}\right)^2=-\frac{627217}{6912}\approx -90.7432$$

A partir de ahora no vamos a trabajar con fracciones por la sencilla razón que vamos a tener que calcular su raíz cuadrada (por cierto, es la raíz cuadrada de un número negativo. Bienvenido a $\mathbb{C}$).

5.- Calculamos el valor de $t$. En este caso $$t=\sqrt[3]{-\frac{a_0}{2}+\sqrt{\Delta}}+\sqrt[3]{-\frac{a_0}{2}-\sqrt{\Delta}}$$

¡¡Espera que así nos salen cuatro soluciones. Bueno, pues debemos elegir los números a operar tales que $\displaystyle \left(\sqrt[3]{-\frac{a_0}{2}+\sqrt{\Delta}}\right)\cdot \left(\sqrt[3]{-\frac{a_0}{2}-\sqrt{\Delta}}\right)=-\frac{a_1}{3}$

No me digas que no es para volverte loco

6.- Tranquilo, te voy a ahorrar líneas y líneas de cuentas; y te doy los valores de $t$ que resuelven la cúbica, además vamos a tener suerte y nos van a salir números reales:

$$\begin{aligned}y_1&=-1.72567\\y_2&=-0.21528\\y_3&=1.94096\\\end{aligned}$$

¿Seguro que lo hemos hecho bien? Bueno, pues podemos pedirle a R que nos dibuje la cúbica a ver si intuimos las soluciones. El código que debes introducir es el siguiente:

ecuacion<-function(x){4x^3-(163/12)x-623/216}
curve(ecuacion,col=2, lwd=3, xlim=c(-3,3), ylim=c(-15,8), xlab="", ylab="", main="Representación de la cúbica")
abline(h=0, lwd=1, lty="dashed")
text(1,6, expression(paste(f(x)==4x^3-frac(163,12)x-frac(623,216))), cex=1.5)

7.- Ahora tenemos que deshacer todos los cambios. Así que primero hacemos $t\rightarrow y$ y luego $y\rightarrow x$.

$t_1=-1.72567\ \longrightarrow \ y_1=-1.55901$

$t_2=-0.21528\ \longrightarrow \ y_2=-0.04861$

$t_3=1.94096\ \longrightarrow \ y_3=2.10763$

Y a partir de los valores de $t$, puedo calcular los valores de $x$, que es la incógnita que realmente tengo que calcular:

$y_1=-1.55901=x+\frac{1}{x}\ \Longrightarrow \ \left\{ \begin{aligned} x_1&=-0.7795+0.6267 i\\x_2&= -0.7795-0.6267 i \end{aligned} \right.$

$y_1= -0.04861 =x+\frac{1}{x}\ \Longrightarrow \ \left\{ \begin{aligned} x_3&=-0.0243+0.9997i\\x_4&=-0.0243-0.9997i\end{aligned} \right.$

$y_1=2.10763 =x+\frac{1}{x}\ \Longrightarrow \ \left\{ \begin{aligned} x_5&=0.7216+0i\\x_6&=0.7216-0i\end{aligned} \right.$

¿Era o no era diabólico este ejercicio? Por esta razón, tu profe que no te tiene manía, no te va a pedir que lo calcules a mano. De hecho, yo ya te he dicho que jamás lo he planteado en enseñanza media y jamás lo plantearé.

Como ves no sólo de Ruffini viven los polinomios, también hay métodos más ingeniosos que nos permiten su resolución y factorización.

Ahora bien, ¿crees que cuando, fuera de un contexto académico y con ejercicios pensados y repensados, te tienes que enfrentar a un polinomio de sexto grado se hace todo esto? ¡¡¡NI LOCO!!! Te vas a un software y el ordenador te lo hacer rápido, bien y sin equivocaciones. Por ejemplo, para R la función que te resuelve cualquier polinomio es

polyroot() 

Pero una cosa no me negarás, este tipo de resolución implica mucha imaginación, ingenio y un poquito de audacia para el primero que dijo «por este camino»

En fin, nada mas por hoy

Si quieres contactar conmigo puedes hacerlo aquí

Si te gusta lo que hago y quieres invitarme a un café ¡¡te doy las gracias por adelantado!!

 Gracias por leerme 

Bibliografía

• Godement, R; 1983; Algebra; Tecnos; Madrid; ISBN: 978-843-090-526-3
• Suprún, V. P.; 2011; Matemática para estudiantes preuniversitarios: Métodos no estándares para la resolucín de ecuacines y desigualdades. 350 problemas detalladamente resueltos; Ed. HAYKA-URSS; Moscú; ISBN: 978-5-369-00369-9 (edición en español)
• Suprún, V. P.; 2011; Matemática para estudiantes preuniversitarios: Problemas de alta dificultad. 300 problemas detalladamente resueltos; Ed. HAYKA-URSS; Moscú; ISBN: 978-5-396-00101-5 (edición en español)