▶ ‼ Ecuaciones exponenciales y logarítmicas 💥

[latexpage]

Este tipo de ecuaciones aparecen a partir de 4ESO. Es verdad que aquellas que se trabajan en 4ESO apenas podrían llegar a denominarse ecuaciones logarítmicas o exponenciales, pues son muy pero que muy sencillas y la mayor dificultad estriba en que la noción de logaritmo es nueva para los alumnos y eso hace que les parezcan muy difíciles.

Mediante este título voy a englobarte ecuaciones donde la incógnita aparece EN un exponente o bien DENTRO de un logaritmo.

Como ya sabrás la expresión $2^3$ es un número real al igual que $\sqrt{5}$ o $8,34^{2,7}$. Supongo que después de leer mi entrada sobre logartimos tampoco tendrás problema en reconocer los siguientes números reales: $\log_4 17$; $\log_{23} 92;$ $\log 34$; $\ln 0,34$

Por lo tanto, en esta entrada nos vamos a centrar en ecuaciones parecidas a las siguientes:

$$\log(2x^2+2)^2=4\qquad\qquad 6^{2x-5}=6^{x-2}$$

La primera ecuación la vamos a llamar de tipo logarítmico y la segunda de tipo exponencial.

En 4ESO los problemas a los que se deben enfrentar los chavales son algunas como: $\log_x5=5$ o $3^2x=81$ pero pasar de estos dos ejemplos a los anteriores es casi inmediato.

Lo fundamental para resolver ecuaciones logarítmicas y exponenciales es SABERSE MUY BIEN LAS PROPIEDADES de los logaritmos

Ecuaciones tipo de 4ESO

Ecuaciones tipo logarítmico para 4ESO

Las ecuaciones que te puedes encontrar en 4ESO son como las que te pongo a continuación. Su resolución es inmediata con sólo aplicar bien la definición, bien las propiedades de los logaritmos:

$$\log_x125=3$$

Según la definición de logaritmo tienes que $\displaystyle x^3=125$ y sin más que factorizar el número $\displaystyle 125 $ obtienes que $x=5$

$$\log_b2\sqrt{2}=\frac{1}{2}$$

Igual que antes, aplicando la definición de logaritmo: $\displaystyle b^{1/2}=2\sqrt{2}$ y sin más que elevar al cuadrado ambas partes del igual obtienes que $\displaystyle b=8$

$$\log_x 5=5$$

Este es igual de sencillo: $\displaystyle x^5=5$ y si ahora sacas la raíz quinta obtienes que $\displaystyle x=\sqrt[5]{5}$

$$\displaystyle {\log_\sqrt{3}.} x=4$$

Este es aún más sencillo, sin más que aplicar la definición: $\displaystyle x=\sqrt{3}^4=9$

Verás que también te piden sumar logaritmos. Aquí debes tener cuidado ya que te deben coincidir las bases de los logaritmos.

$$\log 20+\log 500=¿?$$

Si aplicas la propiedad por la cual la suma de logaritmos es el producto de logartimos obtienes que: $\displaystyle \log 20+\log 500=\log 100000=4$

$$\log_2 200-\log_2 25=¿?$$

Si aplicas la propiedad por la cual la resta de logaritmos es el cociente de logaritmos, obienes que: $\displaystyle \log_2 \frac{200}{25}=\log_2 8=3$

$$\displaystyle \log_8 512+\log_8 4-\log_8 0,125=¿?$$

Ahora simplemente debes aplicar varias veces las propiedades anteriores $\displaystyle \log_8 \frac{512\cdot 4}{0,125}$ $\displaystyle=\log_8 \frac{4096}{1/8}$ $\displaystyle=\log_8 32768$

Hemos llegado así a un número feo $32768$ pero si lo factorizamos tenemos que $32768=2^{15}$ y si ahora ajustamos esta descomposición para que sea una potencia de 8 (date cuenta que estoy buscando una potencia de la base del logaritmo), obtengo que:

$\displaystyle \log_8 32768= \log_8 8^5=5\log_8 8=5$

Un pelín más complicado podría ser el siguiente:

$$\log_4 128$$

En este caso, si factorizas $\displaystyle 128=2^7$ y si lo que buscas es una potencia de 4 (porque 4 es la base de los logaritmos en los que estás trabajando) debes tener un poco más de ingenio:

• Lo que voy a hacer es quitar el 2 y poner un 4. Así voy a tener $\displaystyle 4^7$
• Si sigo así, no estoy calculando el logaritmo que me piden si no su cuadrado ya que $4=2^2$ así que ahora saco la raíz cuadrada de $\displaystyle 4^7$.
• Si pongo todo lo anterior en forma de potencias lo que he hecho ha sido lo siguiente: $\displaystyle 2^7=\left(4^7\right)^{1/2}$ Observa que el exponente $1/2$ se anula con el exponente $2$ que he introducido cambiando el $2^7$ por un $\displaystyle 4^7=\left(2^2\right)^7$

Seguimos:

Tenemos que ya hemos transformado $\displaystyle \log_4 128 = \log_4 \left(4^7\right)^{1/2}$ y ahora sólo hay que aplicar las propiedades de los logaritmos:

$\displaystyle \log_4 \left(4^7\right)^{1/2}= \frac{7}{2} \log_4 4=\frac{7}{2}$

Ecuaciones tipo exponencial de 4ESO

Al igual que pasa con las ecuaciones tipo logaritmo, en 4ESO las ecuaciones exponenciales se resuelven casi a ojo.

$$3^{2x}=81$$

Este tipo de ecuaciones las puedes enfrentar de dos maneras distintas:

• Si factorizas $\displaystyle 81=3^4$ por lo que la solución aparece igualando exponentes y tienes que $\displaystyle x=2$
• Tomando logaritmos. Pero ¿cuáles? Mi consejo es que tomes logartimos en base 3 (¿te imaginas por qué?…. Sí, porque si tomo logaritmos en base 3 resulta que $\log_3 3^4=3$ y plof nos desaparece $\log_3 3$) Así tienes que la anterior ecuación queda: $$\displaystyle \log_3 3^{2x}=\log_3 81=\log_3 3^4 \Longrightarrow 2x\log_3 3=4\log_3 3 \Longrightarrow 2x=4$$ y por tanto llegas a la misma solución que antes.

$$5^{3x}=250$$

Aquí el resultado va a estar dado en función de logaritmos. ¿Que cómo lo sé? porque $5$ es un número primo y si descompongo $250=2^2\cdot 5^3$. Así que si elijo la base 5, me va a quedar en la solución un $\log_5 2$ por algún sitio; y si elijo la base 2, lo que ocurrirá es que me va a quedar un $\log_2 5$ en algún lugar. Por tanto, mi consejo es que elijas trabajar en logaritmos decimales:

$\displaystyle 5^{3x}=250\Longrightarrow 3x\log 5=\log \left(2^2\cdot 5^3\right) \Longrightarrow 3x=\frac{2\log 2+3\log 5}{\log 5}\Longrightarrow x=2\frac{\log 2}{\log 5}+3\approx 3,8614 $

Ejercicio típico de examen

Un ejercicio típico de examen que te vas a encontar es algo parecido al siguiente:

Dados $\log 5=0,69897$ y $\log 11=1,04139$ calcula los siguientes logaritmos sin usar la calculadora: $\log 55$, $\log 550$, $\log 2500$

Estos ejercicios son para saber si te sabes las propiedades del operador logaritmo, y no te los ponen porque tu profe te tenga manía, si no porque las propiedades te las tienes que saber sí o sí. Te los resuelvo a continuación

• $\log 55=\log (5\cdot 11)=\log 5 +\log 11=1,74036$
• $\log 550=\log (55\cdot 10)=\log 55+\log 10=2,74036$
• $\log 2500= \log(5^2\cdot 10^2)=2\log 5+2\log 10=3,39794$

Como ves es un ejercicio muy sencillo si sabes qué te están preguntando. No es raro encontrase a alumnos que protestan porque «¿Cómo voy a hacer esto sin la calculadora?» Pues sí, se puede hacer sin calculadora, y en no más de 4 minutos debes tenerlo hecho. Claro que si no te sabes las propiedades de los logaritmos te pueden dar una hora o un año y no lo vas a sacar…

Vamos a ver ahora qué te puedes esperar si estás cursando bachillerato.

Ecuaciones de tipo logarítmico

Como en cualquier tipo de ecuación, de lo que se trata es de ir despejando la incógnita. Has de tener en cuenta que, por ejemplo $\log 2$ , es un número como otro cualquiera y no te debe distraer. Además, a veces necesitarás tener la perspicacia de transformar un número en un logaritmo, esto es, en vez de poner 1, poner $\log 10$, o en lugar de escribir -3, escribir $\log0,001$ Esto te va a permitir usar diferentes propiedades de los logaritmos.

Al final de lo que se trata es de dejar sola la $x$ a un lado del igual. En este caso, muy probablemente dejarás la $x$ dentro o junto a un logaritmo; pero si llegas hasta ahí sólo tienes que aplicar la definición o una pequeña discusión sobre qué significa la igualdad de logartimos.

Pero como las cosas se ven mejor con ejemplos, vamos a hacer algunas:

Ejemplos

$$2 =\log \frac{x}{2}-\frac{7}{4}$$

Como en cualquier ecuación lo primero es dejar la $x$ sola Lo que pasa es que ahora viene acompañada del operador $\log$

$$\log \frac{x}{2}= 2 + \frac{7}{4} =\frac{15}{4}$$

Ahora piensas: «Jo, si en lugar de una fracción tuviese un logaritmo, podría hacer algo» Pues ya sabes lo que te tienes que preguntar: ¿Para qué número su logaritmo vale $15/4$? Claramente la respuesta es $10^{15/4}$.

Ya lo tienes. Ahora te queda de la siguiente manera:

$$\log \frac{x}{2} =\frac{15}{4}=\log 10^{15/4}$$

Y ya sabes que hay dos números: $x/2$ y $10^{15/4}$ cuyos logaritmos son iguales. Por tanto esos números TIENEN que ser iguales:

$$\frac{x}{2}=10^{15/4}\Rightarrow x=2\cdot 10^{15/4}=2000\sqrt[4]{1000}$$

También podrías haber pensado en aplicar la definción de logartimo en $\displaystyle \log \frac{x}{2} =\frac{15}{4}$ y habrías llegado al mismo sitio $\displaystyle \frac{x}{2}=10^\frac{15}{4}$

$$\log(7x-9)^2+\log(3x-4)^2=2$$

En esta ecuación el primer paso consiste en bajar los exponenetes de las potencias que hay dentro de los logaritmos y en cambiar $2=\log 100=\log 10^2=2\log 10$. Así tenemos que:

$\displaystyle2\log(7x-9)+2\log(3x-4)=2\log 2$

Como cada uno de los sumandos que aquí aparecen está multiplicado por 2, simplemente divido a toda la ecuación por 2 y aplico la propiedad que habla de la suma de logaritmos:

$\displaystyle\log\left[(7x-9)\cdot (3x-4)\right]=\log 2$

Y ahora debes discutir qué ocurre con el igual. Imagina que tenemos dos números $A$ y $B$, de los cuales sabemos qeu $\log A=\log B$. ¿Qué puedes decir de ellos?… Pues que $A=B$ Lo único que ocurre es que no tenemos dos números si no una expresión $(7x-9)(3x-4)$ y un número $2$. Así que decimos si los logaritmos de elllos son iguales, es porque ellos son iguales:

$\displaystyle (7x-9)(3x-4)=2$

Y supongo que resolver esta ecuación de segundo grado no te supone ninguna dificultad, así que te dejo las soluciones:

$
\left\{
\begin{aligned}
x_1=&2\\
x_2=& \frac{13}{21}
\end{aligned}
\right.
$

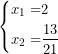
Y ¿ya hemos acabado? Pues no, queda un último paso, y es comprobar que ambos números tienen sentido en la ecuación original. Así que ahora te toca sustituir $\displaystyle x_1; x_2$ en $\log(7x-9)^2+\log(3x-4)^2=2$ y ver si lo podrías calcular. Ya sabes que los logaritmos de números negativos no existen en los reales, por lo que podría ocurrir que alguno de estos dos candidatos a solución implicara que tuvieses que calcular unlogaritmo de un número negativo.

En este caso, ambas posibles soluciones son válidas. Pero no te olvides nunca de comproblarlas.

$$\log x^3=\log 6+2\log x$$

Este es mucho más fácil que el anterior:

$\displaystyle \log x^3=\log 6+2\log x=\log 6x^2$

Y puesto que de dos números sabemos que sus logaritmos son iguales, eso implica que ambos números son iguales y tenemos que:

$\displaystyle x^3= 6x^2$

Ahora debes resolver esta ecuación de tercer grado, pero piensa un poco… es muy sencillo:

$\displaystyle x^3-6x^2=0 \Longrightarrow x^2\left(x-6\right)=0 \ \Longrightarrow \ \left\{ \begin{aligned} x_1=&0\\x_2=&6\end{aligned}\right.$

Ahora debemos comprobar que efectivamente éstas son las soluciones de la ecuación:

• ¿Puede ser $x=0$? No, porque eso implicaría decir que: $\log 0^3=\log 6+2\log 0$ Y como sabes el $\log 0$ no existe, en ninguna base.
• Así que debemos comprobar que la solución es $x=6$, lo que significa que $\log 6^3=\log 6+2\log 6$ Lo cual es verdad.

Por tanto la solución es: $x=6$. Como ves hemos seleccionado dos posibles soluciones ($x=0$ y $x=6$) y luego hemos comprobado cuál de las dos funciona.

$$\log x^3=\log 6+2$$

Este es parecido, pero no igual, al anterior. Verás como la solución es muy distinta:

$\displaystyle \log x^3=\log 6+2=\log 6 +\log 100=\log 600$

Ahora hacemos la misma discusión que antes. Puesto que de dos números sabemos que sus logaritmos son iguales, eso implica que ambos números son iguales:

$\displaystyle x^3=600\Longrightarrow x=\sqrt[3]{600}=2\sqrt[3]{75}$

$$(x^2-x-3)\log 4=3\log\frac{1}{4}$$

Ahora tenemos una ecuación donde antes de nada, vamos a intentar eliminar los $\log 4$. Lo que quiero decir es que en el primer miembro de la ecuación hay un $\log 4$ y me pregunto ¿Podría transformar el segundo miembro de la ecuación en algo que tuviese como factor $\log 4$? La respuesta es sí. Sólo debes tener muy presentes las propiedades de los logaritmos y de las potencias.

$\displaystyle (x^2-x-3)\log 4=3\log\frac{1}{4}\Longrightarrow \log 4^{(x^2-x-3)}=\log 4^{-3}$

Y ya sabes aquello de que si dos números tienen logaritmos iguales es que son iguales:

$\displaystyle 4^{(x^2-x-3)}=4^{-3}$

Y ahora tengo dos potencias de 4 que son iguales, por lo tanto sus exponenetes serán iguales

$\displaystyle (x^2-x-3)=-3$

Que es una ecuación de segundo grado ultrasencilla:

$ \left\{\begin{aligned}
x_1=&0\\
x_2=&1
\end{aligned}\right. $

¿Ahora qué queda por hacer? queda comprobar que estas dos soluciones son válidas en la ecuación original. Así que ya sabes, a sustituir:

Para $x=0$

$\displaystyle (0^2-0-3)\log 4=3\log\frac{1}{4}\quad \longrightarrow 4^{-3}=\left(\frac{1}{4}\right)^3$

Luego SI nos vale.

Para $x=1$

$\displaystyle (1^2-1-3)\log 4=3\log\frac{1}{4}\quad \longrightarrow 4^{-3}=\left(\frac{1}{4}\right)^3$

Luego también nos vale.

$$\log\left(2^{2-x}\right)^{2+x}+\log1250=4$$

Esta ecuación parece mucho más complicada, pero en realidad es exactamente igual que las anteriores:

$\displaystyle \log\left(2^{2-x}\right)^{2+x}+\log1250=4 \longrightarrow \log\left(2^{2-x}\right)^{2+x}=\log \frac{10000}{1250}=\log 8$

Como el primer logaritmo es una potencia de 2 y el segundo término de la ecuación es $8=2^3$, voy a ponerlo todo en función de las potencias de 2, además voy a ir aplicando la propiedad de las potencias que dice potencia de una potencia….:

$\displaystyle \log\left(2^{2-x}\right)^{2+x}=\log 2^3 \Longleftrightarrow 2^{(2-x)(2+x)}=2^3$

Por lo que todo queda en resolver:

$\displaystyle (2-x)(2+x)=3$

Que es una ecuación de segundo grado cuyas soluciones son $x=\pm 1$

Y ahora ¿Qué queda por hacer? Comprobar que estas dos soluciones son válidas. Pero esto ya te lo dejo a tí, no voy a hacerlo yo todo….

Ecuaciones de tipo exponencial

Las ecuaciones de tipo exponencial son aquellas en las que la incógnita aparece EN un exponente. Sin usar herramientas de análisis matemático como son las derivadas, teorema de Bolzano, etc la forma que tenemos de enfretarnos a ellas es bien con un cambio de variable, bien tomando logaritmos en algún momento dado.

Al igual que con las ecuaciones logarítmicas, estas cuestiones se ven mejor con unos ejemplos, así que vamos a hacer alguno:

$$\left3^{2x}=3^6$$

Esta ecuación es trivial, y no tienes más que igualar los exponenetes:

$\displaystyle 2x=6\Longrightarrow x=3$

$$3^x=27$$

Al igual que antes, si tienes en cuenta que $\displaystyle 27=3^3$ todo queda reducido a

$\displaystyle 3^x=3^3 \Longrightarrow x=3$

$$4^x= 0,03125$$

No te creas que esto es imposible. Yo siempre recomiendo a mis alumos que trabajen con fracciones y no con números decimales, así que vamos a calcular la fracción generatriz del segundo miembro de la ecuación:

$\displaystyle 4^x=0,03125= \frac{1}{32}$

Y ahora vamos a buscar una potencia de 4 que sea igual a 32. Pero este ajuste ya lo hemos hecho antes: $\displaystyle 32=2^5 =\left(\left 2^2\right)^5\right)^{1/2}$ Por lo que la ecuación queda como:

$\displaystyle 4^x=4^{-5/2}$

Y una vez que has llegado aquí, la solución es….

$\displaystyle x=-\frac{5}{2}$

$$2^{x+2}=16$$

Esta ecuación ni siquiera tiene truco.

$\displaystyle 2^{x+2}=16=2^4 \Longrightarrow x=2$

$$2^{x+1}+2^{x-1}=20$$

Esta ecuación tiene un pequeño truco. Vamos a hacer un cambio de variable. Es decir, vamos a llamar $\displaystyle y=2^x$ con este cambio de variable lo que pretende es que al final todo me quede en función de una potencia con la misma base. Así puedo escribir la ecuación anterior como

$\displaystyle 2 y +\frac{y}{2}=20$

Y esta ecuación de primer grado tiene por solución $\displaystyle x=\frac{40}{3}$

¿Es esta la solución? No. Ni mucho menos. Aún queda trabajo por hacer. Lo que hemos calculado es $\displaystyle 2^x$ así que ahora toca deshacer el cambio.

$\displaystyle 2^x=\frac{40}{3} \longrightarrow x=\frac{\log \displaystyle \frac{40}{3}}{\log 2}$

Ya casi hemos acabado. De hecho yo casi considero que esta es la solución, porque aunque feo el número $\displaystyle\frac{\log \displaystyle \frac{40}{3}}{\log 2}$ se puede calcular y tiene un valor de $x\approx 3,7370$. Pero si quieres puedes aplicar un poco más las propiedades de los logaritmos y decir:

$\displaystyle x=\frac{\log \displaystyle \frac{40}{3}}{\log 2}= \frac{\log (2^3 \cdot 5)- \log 3}{\log 2}=3+\frac{\log 5-\log 3}{\log 2}$

$$9^{x+1}+3=28\cdot 3^x$$

El primer paso consiste en escribir $9^{x+1}$ como una potencia de 3. Después vamos a hacer el cambio $y=3^x$

$\displaystyle \left(3^2\right)^{x+1}+3 =28\cdot 3^x$

Con lo que aplicando el cambio que te he dicho y reordenando términos tenemos:

$\displaystyle 3^{2x+2}-28\cdot 3^x +3=0\Longrightarrow 9y^2-28y+3=0$

Y las soluciones de esta ecuación son:

$\left\{\begin{aligned}
y_1=&3\\
y_2=&\frac{1}{9}
\end{aligned}\right.$

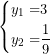
Y ahora queda deshacer el cambio

Para $y=3$ tenemos que $3^x=3$ con lo que la primera solución es $x_1=1$

Para $\displaystyle y=\frac{1}{9}=3^{-2}$ tenemos que la segunda solución es $x_2=-2$

El último paso es comprobar que estas dos soluciones verifican la ecuación original, pero esto ya te lo dejo a ti.

$$2^{3x-1}+4^{2x-2}=8$$

Esta ecuación es complicada, y ya te advierto que no vamos a ser capaces de encontrar todas las soluciones. Pero como lo importante no es aprender cómo resolver esta ecuación en concreto si no cómo aprender a resolver ecuaciones exponenciales, por eso te la he puesto aquí.

Lo primero de todo es intentar poner las $x$ de los exponentes en dos potencias pero con la misma base. La forma más evidente es poner el $4$ de $4^{2x-2}$ en forma de potencia de dos. Y luego operar:

$\displaystyle 2^{3x-1}+\left(2^2\right)^{2x-2}=8\longrightarrow 2^{3x-1}+\left(2\right)^{4x-4}=8\Longrightarrow \frac{2^{3x}}{2}+\frac{ 2 ^{4x}}{4}=8$

Llamamos $y=2^x$ y obtenemos:

$\displaystyle\frac{y^3}{2}+\frac{ y^4}{4}=8\Longrightarrow y^4+2y^3-32=0$

Si pretendes hallar las soluciones de esta ecuación, debes utilizar el algoritmo de Ruffini; y la única solución que serás capaz de encontrar de esta manera es: $y= 2$. Las otras tres soluciones no vas a ser capaz de encontrarlas y no entraremos en ello.

El caso es que ahora tienes un posible candidato a solucion: puesto qeu $y=2$, esto significa que $2^x=2$ por lo que la solución inmediata es $x=1$

Falta el último paso. Comprobar que $x=1$ es efectivamente solución de la ecuación original, pero eso, como siempre te lo dejo a ti.

$$4e^x-5e^{-x}+e^x=0$$

Que no te asuste esta ecuación. Es de las más sencillas que hay en la entrada. Ni siquiera va a hacer falta hacer un cambio de variable.

Lo primero que vamos a hacer es quitarel $e^{-x}$ para ello multiplicaremos a toda la ecuación por $e^x$. Esto lo podemos hacer porque $e^x\neq 0 $ para cualquier valor de $x$. Así tenemos:

$\displaystyle 4e^{2x}-5+3^{2x}=0$

¿Te das cuenta de que la cosa se está poniendo muy interesante? Seguimos:

$\displaystyle 5e^{2x}-5=0\Longrightarrow e^{2x}=1$

¡¡Ajá!! ¡¡Ya lo tenemos!! $x=0$

Y falta el último paso que es… bueno, ya tu sabes…

Ecuaciones con truco

En esta parte de la entrada te voy a mostrar ecuaciones que necesitan algo más que hacer operaciones de una manera mecánica. Para llegar a resolverlas necesitas tener un poco de audacia.

$$3^{4x-2}=9^{-(x+1)}$$

Lo primero que nos gustaría es tener todo en potencias con la misma base. ¿Que te parece si llo poenmos todo en potencias de 3?

$\displaystyle 3^{4x-2}=3^{-2x-2}$

Y ahora discutimos, si dos potencias son iguales y tienen igual base, entonces los exponentes son…. ¡¡exacto!! son iguales.

$\displaystyle 4x-2=-2x-2 \longrightarrow 6x=0\Longrightarrow x=0$

No te olvides de comprobar si esta solución verifica la ecuación original….

$$\displaystyle \sqrt[2-x]{\displaystyle 25^{\frac{2x+1}{2}}}=\frac{1}{5}$$

Para resolver esta ecuación, lo más sencillo es expresar las raíces como una potencia de exponente fraccionario y luego operar:

$\displaystyle \left(25^\frac{2x+1}{2}\right)^{2-x}=5^{-1}$

Como ves la cosa está mejorando bastante. Voy a buscar una potencia de 5.

$\displaystyle 5^{2\cdot \frac{2x+1}{2}\cdot (2-x)}=5^{-1}$

Por lo que al final todo se basa en resolver esta ecuación de segundo grado, que a estas alturas es… bueno, es trivial.

$$(2x+1)(2-x)=-1$$

$$\displaystyle \sqrt[3x]{\displaystyle \sqrt[3]{\displaystyle \sqrt[3x]{9}}}=3^{2x}$$

Si traducimos las raíces a potencias de exponete fraccionario, al final obtenemos:

$\displaystyle 3^{2\cdot 3x\cdot 3\cdot 3x}=3^{2x}$

Y no me dirás que esto es difícil ¿verdad?

$\displaystyle 54x^2=2x\Longrightarrow \left\{\begin{aligned} x_1=&0\\x_2=&\displaystyle \frac{2}{27}\end{aligned}\right.$

$$\left(\sqrt{3}\right)^{\frac{2x}{3}-1}=\sqrt{\displaystyle 9^{\frac{3x-2}{2}}$$

Y ahora tenemos que empezar por….

Bueno, empezamos por ponerlo todo en forma de potencias de base 3:

$\displaystyle 3^{\displaystyle \frac{1}{2}\left(\frac{2x}{3}-1\right)}=3^{\displaystyle \frac{3x-2}{2}}$

Y ya sólo hay que resolver lo siguiente:

$\displaystyle \frac{1}{2}\left(\frac{2x}{3}-1\right) =\frac{3x-2}{2}\Longrightarrow 4x-3=9x-6\Longrightarrow x=\frac{3}{5}$

Como ves todo se basa en operar para quedarnos con una potencia y a partir de ahí decir aquello de: «si dos potencias son iguales, y tienen la misma base; entonces deben tener el mismo exponente»

Y hasta aquí la entrada de hoy. Te advierto que hay ecuaciones exponenciales y logarítmicas que no se resuelven así; de hecho hay bastantes cuya solución sólo se puede obtener de forma aproximada como por ejemplo $x^x=100$ o bien la Ecuación de Colebrook-White la cual conocerás si algún día acabas estudiando hidráulica y mecánica de fluidos.

Lo que he pretendido con esta entrada es darte las herramientas básicas necesarias para enfrentarte a la resolución de algunos tipos de ecuaciones logarítmicas y exponenciales. Si, como de costumbre tienes alguna sugerencia, duda o comentario, por favor, no te olvides de escribirlos más abajo

Si quieres contactar conmigo puedes hacerlo aquí

Si te gusta lo que hago y quieres invitarme a un café ¡¡te doy las gracias por adelantado!!

 Gracias por leerme 

Bibliografía

• Aparicio Peñas, A. M., Arribas Ruiz, F., González García, C., Llorente Medrano, J., Ruiz Jiménez, M.; 2015; Matemáticas aplicadas a las ciencias sociales (I); Ed. Editex; Madrid; ISBN: 978-84-9078-504-1.
• Argüeso, M., Borobia, N., Lázaro, O., Pajares, A., Tomeo, V.; 2015; Matemáticas aplicadas a las ciencias sociales (I); Ed. Paraninfo; Madrid; ISBN: 978-84-283-3548-5.
• Colera Jiménez, J., Oliveira González, M. J., Gaztelu Albero, I., Colera Cañas, R.; 2016; Matemáticas aplicadas a las enseñanzas académicas, 4 ESO; Ed. ANAYA; Madrid; ISBN: 978-84-698-1069-9.
• Fernández del Campo y Sánchez, J. E.; 1985; Problemas de matemáticas: soluciones razonadas 2ºBUB; Editorial Magisterio Español; Madrid; ISBN: 84-268-1534-7.
• Vizmanos Buelta, J. R., Anzola González, M., Primo Martínez, A.; 1987; Funciones-1: matemáticas 1ºBUP; Ediciones SM; Madrid; ISBN: 84-348-0943-5.