⏩ Regla de los signos📏 - Mi profe me tiene manía

La regla de los signos te va a permitir operar las multiplicaciones y divisiones de números donde intervienen números negativos. Y no se trabaja en clase porque tu profe te tenga manía, es que es muy importante que aprendas a manejarla y no dudes cuando operas con ella; tienes que tatuártelo en la memoria.

Antes de nada te tengo que repetir:

La regla de los signos solo sirve para cuando estés trabajando con multiplicaciones o divisiones

Me imagino que ya conocerás de sobra las tablas de multiplicar. Pero si te has dado cuenta, siempre son números positivos, ¿Qué ocurre si esos números que multiplicas no son positivos? ¿Y si uno es positivo y otro es negativo?

Pues todo esto se resuelve con la regla de los signos . Una explicación técnica puedes verla en mi entrada sobre ello, pero te advierto que no es un nivel de ESO.

Supongo que en clase te habrán enseñado esta tabla o alguna parecida:

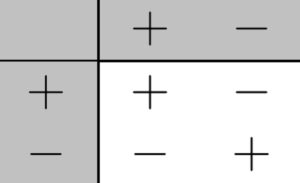
Tabla resumen de la regla de los signos — Regla de los signos

Te voy a enseñar a leer esta tabla.
Cuando quieres multiplicar o dividir dos números, lo primero en que te tienes que fijar es en el signo que le acompaña (que son la fila y columna en gris). Luego simplemente tienes que ir cantando de la siguiente manera:

Más por más es más.
Más por menos es menos.
Menos por más es menos.
Menos por menos es más.

Hay quien resumen la regla de los signos diciendo:

Signos iguales, positivo.
Signos distintos, negativo.

Y lo mismo para la división , porque ya sabes… dividir es multiplicar por el inverso. Pero como todo se ve mejor con un ejemplo, aquí van unos cuantos.

Regla de los signos y multiplicación

Ejemplo 1

$(+3)\cdot (+4)=+12$

Primero multiplico $3\cdot 4$ y obtengo el $12$ . Luego decido el signo diciendo más por más es más.

Observa, además, que solo escribo paréntesis para evitar que aparezcan un por « $\cdot$ » y un más « $+$ » seguidos.

Ejemplo 2

$(+3)\cdot (-4)=-12$

Primero multiplico $3\cdot 4$ y obtengo el $12$ . Luego decido el signo diciendo más por menos es menos.

Observa, además, que solo escribo paréntesis para evitar que aparezcan un por $\cdot$ y un menos $-$ seguidos.

Ejemplo 3

$(-3)\cdot (+4)=-12$

Igual que antes, lo primero que hago es multiplicar los números $3\cdot 4$ y luego decido el signo diciendo menos por más es menos.

Ejemplo 4

$(-3)\cdot (-4)=+12$

En este último ejemplo multiplicamos dos números negativos. Ocurre lo mismo, si multiplico $3\cdot 4$ , obtengo $12$ y para decidir el signo digo: menos por menos es más.

Estos ejemplos te los he marcado siempre con los mismos números, $3$ y $4$ , pero he ido cambiando sus signos para que te des cuenta de que el resultado varía de acuerdo a los signos que tengan los factores. Ahora vamos a hacer lo mismo con la división.

Regla de los signos y división

Como te he dicho antes, ahora vamos a dividir números y vamos a ver qué pasa con los signos. Voy a hacer el ejemplo con el número $18$ y lo voy a dividir por $3$ . Además, voy a ir cambiando sus signos para ver qué pasa.

Ejemplo 5

$(+18):(+3)=6$

En este caso, lo primero que hago es dividir los números y digo: «dieciocho entre tres, da seis» y luego me ocupo del signo: «más entre más, es más«

Ejemplo 6

$(+18):(-3)=-6$

Como en el ejemplo anterior, lo primero que hago es dividir los números y digo: «dieciocho entre tres, da seis» y luego me ocupo del signo: «más entre menos, es menos»

Ejemplo 7

$(-18):(+3)=-6$

¿A qué no sabes qué es lo primero que hago?… Efectivamente, lo primero que hago es dividir los números y digo: «dieciocho entre tres, da seis» y luego me ocupo del signo: «menos entre más, es menos»

Ejemplo 8

$(-18):(-3)=6$

Y por último ¿qué es lo primero que voy a hacer?. Como no lo primero que hago es dividir los números y digo: «dieciocho entre tres, da seis» y luego me ocupo del signo: «menos entre menos, es más»

Espero que con estos ejemplos te haya quedado claro como dividir números y espero que recuerdes que:

Por un lado tienes que operar los números y por otro lado tienes que operar los signos

Regla de los signos y fracciones.

Ahora vamos a complicarlo un poco más y vamos a introducir fracciones en las operaciones. Te voy a dar dos ejemplos de multiplicación y dos ejemplos de división. Si no recuerdas cómo se opera con números racionales aquí puedes ver cómo se multiplican o dividen fracciones.

Ejemplo 9

$\frac{2}{3}\cdot \frac{15}{14}=\frac{30}{42}=\frac{5}{7}$

En este caso, tenemos que multiplicar dos fracciones que son positivas, así que lo primero que hago es multiplicarlas y hallo el numerador ( $2\cdot 15=30$ ) y el denominador ( $3\cdot 14=42$ ). El signo lo calculo con la regla de los signos «más por más es más».

Finalmente tengo que simplificar la fracción hasta que sea irreducible, por lo que consigo el resultado de $\displaystyle \frac{5}{7}$

Ejemplo 10

$\frac{4}{5}: \left(-\frac{8}{25}\right)=\frac{4}{5}\cdot \left(-\frac{25}{8}\right)=-\frac{100}{40}=-\frac{5}{2}$

En este caso hay que dividir una fracción positiva entre otra negativa:

Lo primero que hago es calcular el inverso del divisor, es decir, calculo el inverso de $\displaystyle\frac{8}{25}$ que es $\displaystyle\frac{25}{8}$ . Así dejo la división «convertida» en una multiplicación. Ya sabes eso de que dividir es multiplicar por el inverso…
Después del segundo igual, lo que hago es multiplicar numeradores, $4\cdot 25=100$ , y denominadores, $5\cdot 8=40$ .
Ahora ya solo tengo que decidir el signo. Es decir digo: «más por menos es menos».
Lo último que debo hacer es simplificar la fracción que será negativa.

Y así es como se obtiene:

$-\frac{5}{2}$

Ejemplo 11

$-\frac{2}{3}\cdot \frac{6}{5}=-\frac{12}{15}=-\frac{4}{5}$

Ahora tenemos que multiplicar una fracción negativa por una positiva:

Lo primero es multiplicarlas y calcular el numerador, $2\cdot 6=12$ , y el denominador, $3\cdot 5=15$ .
Después solo hay que calcular el signo de esta nueva fracción y digo: «menos por más es menos»
Por último simplifico la fracción que he obtenido y así consigo el resultado, que será negativo: $\displaystyle-\frac{4}{5}$

Ejemplo 12

$-\frac{1}{2}:\left(-\frac{1}{3}\right)=-\frac{1}{2}\cdot (-3)=+\frac{3}{2}$

El último ejemplo es dividir dos fracciones que son ambas negativas:

Primero calculo el inverso de la segunda fracción (la que divide, el divisor). Como la fracción es $\displaystyle-\frac{1}{3}$ su inverso es $\displaystyle-\frac{3}{1}$ . Es decir, $-3$ .
En un segundo paso calculo el numerador, $1\cdot 3=3$ y el denominador $2$ . Así ya solo tengo que calcular el signo y lo hago así: «menos por menos es más».
Así, la fracción que obtenemos es $\displaystyle\frac{3}{2}$ (te he escrito el signo $+$ para que quede claro que es positiva, pero no es necesario). Y como resulta que $\displaystyle \frac{3}{2}$ es una fracción irreducible, éste es el resultado.

Y tú, ¿te lo han explicado de otra forma en la escuela?, ¿te resultó difícil habituarte a la regla de los signos? Anímate y déjame tus respuestas a estas preguntas o cualquier otra impresión en los comentarios

Gracias por leerme

Si quieres contactar conmigo puedes hacerlo aquí

Si te ha gustado lo que has leído y quieres invitarme a un café ☕, te doy las gracias por adelantado.

Vida de la entrada:

– 2020-08-17: Publicación.
– 2020-09-03: Corrección erratas. Añadido botón Paypal.